4 - дәріс Ақпаратты кванттау
Дәріс жоспары:
1. Ақпаратты дискреттеу есебінің жалпы қойылымы;
2. Үздіксіз хабарламаларды шектеулі дискреттеу;
3. Үздіксіз сигналды қайта қалпына келтіру әдістері,
4. Дискреттеу процесінде интерполяцияның Лагранж көпмүшелері,
5. Сигналдарды жеңгей бойынша кванттау.
Уақыт бойынша дискреттеу – үздіксіз хабарламаны, оның уақыттың дискретті мезетінде алынған мәнінің (санақтарының) тізбегімен ауыстырылуы болып саналады. Мұндай
ауыстыруда дискреттеу интервалының ішінде барлық
үздіксіз функцияның мәндерінің жиынтығы жоғалып кетеді. Осылай құрылған функция, уақыттың дискретті мезетінде санақтардың тізбегімен анықталады.
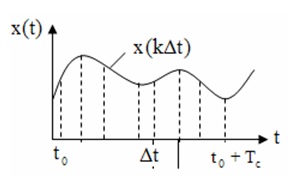
1.1-Сурет - Уақыт бойынша хабарламаны дискреттеу
Адаптивті дискреттеудің теориялық зерттеуі және тәжірибелік іске асыруы көп қиындықтар туғызады. Мысалы, дискреттеу құрылғыларын айтарлықтай іске асыру қиынға түседі, өйткені дискреттелетін хабарлар туралы кең көлемді априорлық мәліметтер керек болады.
Бірқалыпты дискреттеу кең таралған. Бұл дискреттеудің теориясы мен техникасы жеткілікті іске асырылған.
Жоғарыда келтірілген шартқа сай, дискреттеуді (жоғарғы берілген қатынастың бүтін бөлігі алынады) шектеулі (оптимальды) деп аталады. Сонымен қатар, берілген дәлдікпен дискретті санақтардың минимальды санымен, үздіксіз хабарламаның көрінісі қамтамасыз етіледі.
Сигналдарды дискреттеу мәселесі өте күрделі зерттеулер санынының көптігіне қарамастан, оның мәселелерінің түгел шешілуі мүмкін емес.
Қазіргі кезде үздіксіз хабарламаларды шектеулі дискреттеуде В.А. Котельниковтың теоремасы кең қолданылады.
Бұл теореманың бастапқы қалпына тоқтайық. Дискреттеу теориясын құру үшін хабарламаның кейбір моделіне сүйену қажет. Айталық, мүмкін үздіксіз хабарлардың жиынтығына сәйкес келетін {x(t)} квазистационарлы кездейсоқ процестің x(t) -ның бір реализациясы көрсетілген делік.
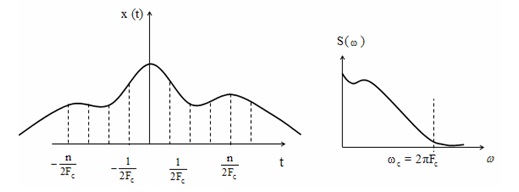
1.2-сурет - Дискреттелетін сигнал және оның спектрі
Белгілі бір (соңғы) уақыт аралығындағы F = 50 Гц жиіліктегі синусоидальды кернеуді кванттау кезінде t мәнін табыңыз. Функцияны қалпына келтіру кезіндегі қателік = 1 %.
Шешуі:
Синусоидалы сигнал кезеңі:
T = 1/F= 1/×50) = 0,02с = 20 мс
Кванттау қадамы:
![]()
Яғни, идеалды жағдайда синусоиданың әрбір жарты толқынын тек бір мәнмен беруге болады.
Сызықтық интерполяция үшін Л коэффициенті:
![]()
Қадамдық интерполяция үшін
коэффициент st және кванттау қадамы ![]() сәйкес болады:
сәйкес болады:
![]()
Қазіргі уақытта техникалық қосымшаларда үздіксіз хабарламалардың дискреттеу интервалы, олардың санақтары бойынша ыңғайлылық пен қарапайымдылықты қайта қалпына келтіру талабымен айтарлықтай анықталады.
Дискреттеу процесінде (n+1) шектеулі туындылары бар x( t ) үздіксіз функция n дәрежелі көпмүшемен аппроксимацияланады.
Сигналды қайта қалпына келтірудің таңдалған әдісіне байланысты, көпмүше интерполяциялаушы немесе экстраполяциялаушы болуы мүмкін. Минимальды қателікті қамтамасыз ету есебі әдетте, сигналды қалпына келтіруде қойылмайды, оның мүмкін қателігі көрсетіледі.
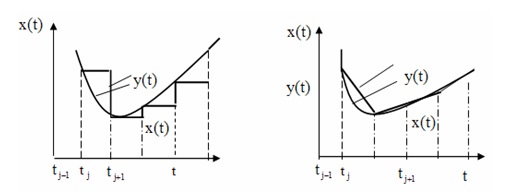
1.3-сурет - Сатылы аппроксимация
Кодтау. Кейінгі түрлендірудің жүзеге асыру ыңғайлығы, дискретті сигналды кодтауын қажет етеді.
Сандардың позициялық формадағы жазбасының мысалы біз қолданатын форма болып саналады (сандардың араб формасы). Осылай, 123 және 321 сандарында 3 цифрының мәні, мысалы оның сандағы орнымен байланысты: бірінші жағдайда үш бірлікті білдірсе (яғни, жай үш), екіншіде – үш жүздікті білдіреді.
Римдік сандар – сандардың құрылуының жартылай позициялық жүйесінің мысалы болып саналады: осылай, IX және XI сандарындағы I белгісі екі жағдайда да бірлікті білдіреді (позициялық емес). Бірақ, Х (онды белгілейтін) белгісінің сол жағында болса, ол оннан алынады, ал оң жақта – ол онға қосылады. Бірінші жағдайда, санның толық мәні 9-ға тең, екіншісінде – 11.
Қазіргі ақпаратта үш санау жүйесі қолданылады (барлығы – позициялық): екілік, он алтылық және ондық.
Екілік санау жүйесі – дискретті сигналдарды кодтауға есептеу кезінде техникада қолданылады. Екілік сигналды аппараттық құрылғымен келтіру, жай нәрсе. Бұл санау жүйесінде, санды келтіру үшін екі таңба қолданылады – 0 және 1.
Он алтылық санау жүйесі – дискретті сигналды кодтауға қолданылады, оның тұтынушысы, жақсы дайындалған пайдаланаушылар – ақпараттар саласындағы мамандар. Мұндай формада операциялық жүйенің интегралданған бөлшегі арқылы сұралған кез келген файлдың мазмұны көрсетіледі. Санды көрсету үшін қолданылатын таңбалар – 0-ден 9-ға дейінгі ондық сандар және латын алфавитінің әріптері – A, B, C, D, E, F.
Ондық санау жүйесі де дискретті сигналды кодтауға қолданылады. Оның тұтынушысы жақсы дайындалмаған пайдаланаушылар – ақпараттар саласындағы мамандар емес (кез келген адам мұндай тұтынушы бола алатыны анық). Санды көрсету үшін қолданылатын таңбалар – 0-ден 9-ға дейінгі цифрлар.
· екілік сандар үшін – санның оң жағындағы төменгі индекс 2 цифр түрінде немесе В әріпі не b (binary – екілік), әйтпесе B мен b таңбалары санның оң жағында көрсетіледі. Мысалы, 1010002 = 101000b = 101000B = 101000B = 101000b;
· он алтылық сандар үшін – санның оң жағындағы төменгі индекс 16 саны немесе H әріпі, не (h) (hexadecimal – он алтылық) түрінде немесе H не (h) таңбалары, санның оң жағында көрсетіледі. Мысалы, 3AB16 = 3ABH = 3ABh = 3ABH = 3ABh.
Сандарды бір санау жүйесінен басқасына аудару үшін арнайы ережелер бар. Олар санның форматына байланысты ажыратылады – бүтін немесе дұрыс бөлшек. Нақты сандар үшін бүтін сан мен дұрыс бөлшекке арналған аудару ережесінің комбинациясы қолданылады.
Бүтін сандарды аудару ережесі. Бүтін санды аудару ережесі, әрқашан бүтін санды береді.
Ондық санау жүйесінен екілік және он алтылық санау жүйесіне аудару:
а) бастапқы бүтін сан, аударылатын санау жүйесінің негізіне бөлінеді (екілік санау жүйесіне аударуда 2-ге немесе он алтылық санау жүйесіне аударғанда 16-ға бөлінеді); дербес және қалдық шығады;
ә) егер шыққан дербес аудару, орындалып жатқан санау жүйесінің негізінен аз болса, онда бөлу процесі тоқтатылып а) қадамына көшеді. Өзге жағдайда дербеске – ә) қадамында сипатталған әрекетті орындайды;
б) барлық шыққан қалдықтар, соңғы дербес аудару орындалатын санау жүйесінің аудару кестесіне сәйкес цифрға түрлендіреді;
в) нәтижелейтін сан құрылады: оның жоғарғы разряды – шыққан соңғы дербес, әрбір келесі кіші разряд соңғысынан басталып, біріншісімен аяқталатын бөлуден шыққан қалдықтардан құрылады. Осылайша, шыққан санның кіші разряды – бөлуден алынған бірінші қалдық, ал үлкен разряды – соңғы дербес.
Қабылдау жағында уақыт бойынша квантталған функцияны қадамдық немесе сызықтық интерполяция немесе Котельников әдісі арқылы қалпына келтіруге болады. Көбінесе сатылы интерполяция қолданылады және ең сирек – Котельников бойынша сүзу. 4.3 а-суретте көрсетілген қадамдық интерполяция келесі мән пайда болғанға дейін (ti) функциясының мәндерін сақтайтын сақтау құрылғыларымен орындалады (ti+1).
1.4-суретте қадамдық интерполяцияның қателігі көрсетілген.
Интерполяция қателігі кезінде I-дің айырымы сол уақытта алынған қалпына келтірілген және бастапқы сигналдардың лездік мәндері арасында қабылданады. Максималды қателік нүктелерде пайда болады 1', 2',...,5'. Жалпы жағдайда бұл қатенің орташа квадраттық мәндері беріледі.
![]()
Котельников бойынша квантталған функцияны қалпына келтіру кезінде сіз алдыңғы және кейінгі барлық дискретті нүктелерді білуіңіз керек. Кейінгі нүктелерді білу ақпаратты беруде кешігуге мүмкіндік беретін жүйелерде ғана мүмкін болады. Автоматты басқару жүйелерінің көпшілігі нақты уақыт режимінде жұмыс істейді және артта қалуға жол бермейді. Мұндай жүйелерде қадамдық интерполяцияны қолдану керек.
Сызықтық интерполяция кезінде сіз кем дегенде бір нүктені алдын-ала білуіңіз керек, бұл кем дегенде кванттау қадамына тең уақытқа кешігуге әкеледі.
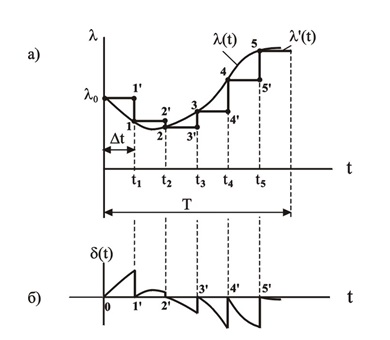
1.4-сурет - Хабарламаны уақыт бойынша кванттау
Дегенмен, нақты сигнал көздерінің қасиеттеріне және нақты арналардың өткізу қабілеттілігінің шектелуіне байланысты белгілі бір дәлдік дәрежесі бар сигнал спектрін кейбір fmax шекті жиілігімен шектеуге болады. Ол әдетте энергетикалық критерий негізінде анықталады. Спектр сигнал энергиясының басым бөлігі (80-95%) шоғырланған 0-ден Fmах-қа дейінгі жиілік аймағымен шектеледі. Спектрдің мұндай шектелуі, әрине, сигналдың бұрмалануына әкеледі.
Сигналды ойнатудың салыстырмалы дәлдігін қатынастан анықтауға болады:
![]()
мұндағы p – сигналдың тасталған жоғары жиілікті компоненттерінің энергиясы;
ДК-сигналдың толық энергиясы.
Осылайша, Котельников теоремасы бойынша алынған есептеулер бойынша уақытпен шектелген сигналды қалпына келтіру сигнал спектрін мәжбүрлі түрде шектеген жағдайда ғана мүмкін болады.
Котельников теоремасын практикалық қолдану үшін түзетілген келесі формуланы қолдануға болады:
![]()
Мұндағы коэффициент функцияның қайталану дәлдігіне және интерполяция әдісіне байланысты. Сызықтық интерполяция кезінде:
![]()
мұндағы қателік-салыстырмалы қателік.
Қадамдық интерполяция кезінде:
![]()
Егер Котельников теоремасында уақыт интервалын түсіндірсек т кванттаудың белгілі бір жиілігінің периоды ретінде Fкв = 1 / rate t, онда кванттау жиілігін сигнал спектрінің максималды жиілігімен байланыстыратын қатынасты алу қиын емес:
![]()
Сигналды цифрлық түрге түрлендіру процесінде Котельников критерийі өте кең қолданылады.