2 - дәріс Ақпаратты өлшеу
Дәріс жоспары:
1. Ақпараттың құрылымдық мөлшері;
2. Геометриялық өлшем;
3. Комбинаторлық өлшем;
4. Аддитивтік Хартли өлшемі;
5. Ықтималдық және ақпарат;
6. Біріккен және шартты энтропия;
7. Дифференциалдық энтропия.
Ақпарат теориясының маңызды сұрағы ақпараттың саны мен сапасын өлшеу мөлшерін орнату болып саналады.
Ақпаратты өлшеу мөлшері ақпарат теориясында үш негізгі бағытта жүргізіледі:
1. Құрылымдық теория – массивтердің дискреттік құрылымын қарастырып, ақпараттық элементтердің (кванттар) қарапайым есептеуі бойынша, өлшеу немесе ақпараттар массивтерінің қарапайым кодтауды болжайтын комбинаторлық әдістер.
2. Статистикалық теория – энтропия түсінігімен хабарла- маның анықталмағандығын, олардың болуының ықтималдығын, демек сол немесе басқа хабарламалардың ақпараттылығы.
3. Семантикалық теория – ақпараттың қажеттілігін, пайдалылығын немесе маңыздылығын, мақсаттылығын ескереді.
Геометриялық әдіс арқылы ақпараттың санын анықтау – сызықтың ұзындығын өлшеу, ауданын немесе дискретті бірлік – кванттар түріндегі берілген ақпараттық кешенінің геометриялық моделінің көлеміне сәйкес келеді. Ақпараттық элементтер ішінде нақты ақпараттық кешеннің дискретті модельдерінде, ақпараттың бөлінбейтін бөлігі – кванттары, сонымен қатар сандық жүйеде – алфавит элементтері бар.
Геометриялық әдіс арқылы потенциалдық, яғни құрылымдық габариттер түріндегі ақпарат мөлшерінің максимальды мүмкіндігі анықталады. Ол толығымен ақпараттық жүйенің зерттелетін бөлігінің, ақпараттық сыйымдылығын көрсетеді. Ақпараттық сыйымдылық, барлық өлшемдер бойынша дискреттік мәндерінің қосындысымен есептеледі.
Комбинаторлық өлшемге әртүрлі комбинациялар көмегімен ақпаратты тасымалдаудың мүмкіндігін бағалауы қажет болған жағдайда, мақсатқа лайықты келу керек. Бұл ақпаратты кодтаудың бір формасы.
Комбинаторлық өлшемде ақпарат саны, элементтердің комбинациясының саны сияқты есептеледі. Яғни, әртүрлі потен циалды құрылымды ақпараттық кешендердің комбинациясын бағалауға ұсынылады.
Ақпарат теориясында сандар мен кодтардың комбинаторикасы маңызды рөл атқарады. (l) санның ұзындығы мен (h) тереңдігі түсінігін енгізейік.
Санның (h) тереңдігі, қабылданған алфавитте болатын әртүрлі элементтердің саны болып аталады. Санның тереңдігі [14,15] кодтау және санау жүйесінің негізіне сәйкес келеді.
Санның (l) ұзындығы сан ұяшығының мөлшері деп, алфавитте керекті өлшем санын ұсынуға қажетті, әрі жеткілікті
қайталану санын айтады. Санның ұзындығы кодтау мен санаудың әртүрлі жүйесін хабарлайды.
(l) ұяшық – алфавитінің бір жиынтығы (l) ұзындықты бір толық санды сақтайтын және бейнелей алатын бір сандық топты құрайды. N санының кейбір мөлшері сандық өрісті ұсынады.
Егер разрядтардың саны (санның (l) ұзындығы) бірге тең болса, онда екілік санау жүйесі (тереңдігі h=2 ) түрінде болады және екілік логарифм орындалады десек, ал ақпараттың потенциалдық саны 1 битке тең (log22=1).
1-қосымшада 1-ден 128-ге дейін сандардың екілік логарифмдері берілген. Бұл, қабылданған жүйедегі өлшемнің бірлігі болып саналады. Ол болатын немесе болмайтын бір қарапайым оқиғаға сәйкес келеді. Аддитивті өлшем (l) санына салыстырмалы I пропорционалдылығын есептеу мүмкіндігін қамтамасыз етуімен қолайлы.
Ықтималдық түсінікте ақпарат кездейсоқ оқиғалардың нәтижесі, кездейсоқ мөлшерлер мен функциялардың орындаулары туралы хабарлама түрінде қарастырылады. Ал ақпарат саны осы оқиғалардың, мөлшерлердің, функциялардың априорлық ықтималдылығына байланысты қойылады.
Айталық, хабарламаның ақпарат көзі әр уақыт кезеңінде кездейсоқ тәсілмен көптеген мүмкіндіктің соңынан біреуін қабылдай алады. Әр ақпарат көзінің қалыпына Х шартты таңба түрінде қойылады. Ақпарат көзінің мүмкін болатын N жағдайына сәйкес келетін x1, x2 , …, xi , ..., xN таңбалардың жиынтығын – алфавит деп атайды, ал алфавиттің көлемі N жағдайдың саны. Мұндай ақпарат көзінен хабарламаларды формальдау xi жағдайдының кейбір таңдауларына және сәйкес келетін таңбаны беруге апарады. Сонымен қатар, қарапайым дискретті хабарлама ретінде дискретті ақпарат көзінен берілетін xi символын түсінеміз. Ақпарат көзінің жеке жағдайы басқаларына қарағанда онымен жиі таңдала алады. Сондықтан жалпы жағдайда, Х ақпарат көзі оқиғаларының ықтималдықтарының қосындысы 1-ге тең жағдайлардың жиынтығымен анықталады.
Энтропия анықсыздық сияқты адамның психологиялық реакцияларын зерттеу кезінде алынатын, сонымен қатар реакция таңдауымен экспериментік мәліметтермен келіседі. Тізбектеп ретсіз кезектесетін тең ықтималды тітіркендіргіштерінің (мысалы, жанатын лампочка) қатесіз реакция уақытының саны, энтропия сияқты санының артуымен өседі. Бұл уақыт бір тітіркендіргіштің таңдауының анықсыздығын (белгісіздігін) сипаттайды.
Тең ықтималды тітіркендіргіштерді, тең ықтималды еместермен ауыстыру кезінде орташа реакция уақыты энтропия қанша кішірейсе, сонша төмендеуге әкеледі.
Жадысыз дискретті екілік ақпарат көздерінің мәні ерекше, себебі көптеген жағдайларда олардың көмегімен мәліметтерді тасымалдау процесін сипаттауға болады.
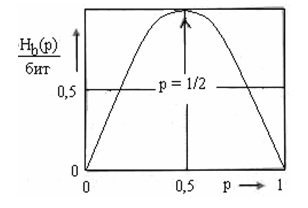
2.1-сурет - Екілік Ақпарат көзінің энтропиясы
Дифференциалдық энтропияның негізгі қасиеттері:
а) егер U кездейсоқ шаманың мүмкін болатын мәндері аймағының жалғыз ғана α , β шегі болса, онда дифференциалдық энтропияның мәні максимальды болса, осы аймақтағы шаманың ықтималдықтарының үлестірімі біркелкі болады.
ә) егер U үздіксіз кездейсоқ шаманың мүмкін болатын мәндерінің аймағына шектеу болмай, бірақ оның дисперсиясы шектеулі екені белгілі болғандықтан, максимальды дифференциалдық энтропияға нормальды үлестірімді U шамасы болады.