Тема 15. Основы цифровой обработки сигналов
План лекции
1. Основные понятия
2. Основы реализации цифровых фильтров
3. Структурная схема построения ЦФ. Каноническая схема реализации ЦФ.
4.Синтез цифровых фильтров
Под цифровой обработкой сигналов (ЦОС) понимают операции над дискретными во времени величинами (отсчетами сигналов). Дискретную величину, поступающую на вход устройства ЦОС в n-ый момент времени (n=0,1,2,…), обозначим x(n). Дискретную величину, получаемую на выходе устройства ЦОС в n-й момент времени, обозначим y(n). Обычно входные величины поступают на устройство ЦОС и выдаются этим устройством с неизменным шагом Δ. Тогда можно записать:
x(n)=x(nΔ), y(n)=y(nΔ).
Чаще всего Δ<1/2Fв является шагом равномерной дискретизации непрерывного сигнала x(t), поступающего на обработку.
Сигналы на входе и выходе современных ЦОС дискретны не только во времени, но и квантованы по уровню, т.е. являются цифровыми сигналами. Однако, в основном мы будем рассматривать работу ЦОС только с дискретными сигналами (так проще и нагляднее), а в конце этого раздела обсудим погрешности, возникающие в устройствах ЦОС из-за квантования дискретных сигналов по уровню.
ЦОС имеет ряд существенных преимуществ перед аналоговой обработкой сигналов:
1) Достигается значительно более высокая точность обработки сигналов по сложным алгоритмам;
2) Возможна гибкая оперативная перестройка алгоритмов обработки сигналов, обеспечивающая как создание многорежимных устройств, так и реализацию адаптивных (подстраивающихся) систем;
3) Достигается высокая технологичность изготовления устройств ЦОС, связанная с отсутствием необходимости настройки при изготовлении и регулировки в процессе эксплуатации;
4) Обеспечивается высокая степень совпадения и повторяемости характеристик реализованных устройств с расчетными характеристиками;
5) Существуют большие возможности автоматизации проектирования устройств;
6) Обеспечиваются высокостабильные эксплуатационные характеристики устройств ЦОС.

Структурно одноканальную систему передачи сообщений (как непрерывных, так и дискретных) с использованием устройств ЦОС на передаче и приеме можно представить следующим образом
Структурная схема передачи сообщений с использованием устройств ЦОС.
ЦФПС - цифровой формирователь первичного сигнала;
ЦМ - цифровой модулятор;
ЦПФ - цифровой полосовой фильтр;
ЦД - цифровой детектор (демодулятор);
ЦФНЧ - цифровой фильтр нижних частот;
ЛС - линия связи.
В системах передачи непрерывных сообщений (в том числе и цифровыми методами) помимо отмеченных на рисунке функций решаются и задачи цифрового компандирования первичного сигнала на входе модулятора (сжатия динамического диапазона) и цифрового эспандирования (расширения динамического диапазона) сигналов на входе детектора.
Наиболее широкое применение нашли линейные устройства ЦОС, в которых сигналы входа и выхода связаны линейными соотношениями. Такими являются все фильтры в рассмотренной схеме, а также схемы ЦМ и ЦД, построенные на основе перемножения двух функций. Кроме того, практически все ЦФ являются стационарными устройствами (свойства не зависят от времени).
![]()
В общем случае в линейном стационарном
цифровом фильтре k-й выходной отсчет y(k) (в момент времени t=kΔ) линейно зависит от k-го входного отсчета x(k) и некоторого количества предшествующих отсчетов x(![]() ) (
) (![]() <k), а
также от некоторого количества выходных отсчетов y(
<k), а
также от некоторого количества выходных отсчетов y(![]() )
(
)
(![]() <k):
<k):
Числа L и M в разностном уравнении (52) называют соответственно относительной памятью ЦФ по входу и выходу. ЦФ с памятью по входу называются рекурсивным, а без такой памяти нерекурсивными.
Алгоритмы работы различных ЦФ отличаются параметрами Q и M и набором коэффициентов {aℓ} и {bi}. Рассмотрим сначала реализацию нерекурсивных ЦФ, когда все bi=0 (т.е. М=0).
В этом случае разностное уравнение (52) принимает вид:
Структурная схема ЦФ, реализующая алгоритм (53) приведена на следующем рисунке:
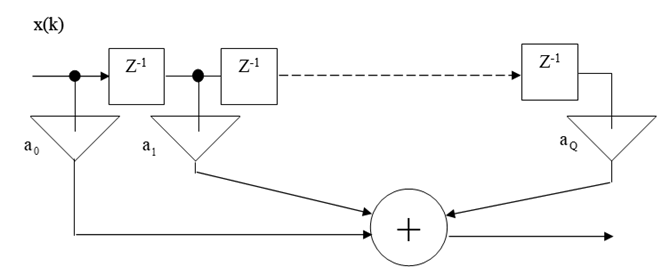
Большое практическое значение имеют методы синтеза ЦФ с требуемым видом импульсной или частотной характеристик ЦФ. Рассмотрим некоторые приемы синтеза ЦФ по заданным характеристикам их аналоговых прототипов.
ЦФ строится с импульсной характеристикой, которая является результатом дискретизации g(t), т.е. ее k-й отсчет g(k)=g(kΔ). Если в импульсной характеристике Цф ограничится конечным числом слагаемых, получаем реализацию в виде трансверсального фильтра. При неограниченном числе компонент g(k) следует реализация в виде рекурсивного фильтра.
Основными элементами ЦФ являются блоки задержки отсчетных значений на один тактовый интервал (условно обозначены символом z-1), а также масштабные блоки aq (усилители). Сигналы с последних собираются в сумматор, образуя входной отсчет. Посредством разностного уравнения (53) можно построить лишь ЦФ с финитной (конечной) импульсной характеристикой {g(0), g(1)…g(Q)}.Если на вход схемы трансверсального типа подать единичный импульс (1,0,0,0,…), то по определению отклик ЦФ есть его импульсная характеристика g(t). Это возможно лишь при условии, что в трансверсальном ЦФ отсчеты импульсной характеристики g(q) совпадают с коэффициентами aℓ, ℓ=0,1,2,…Q.
Взяв Z-преобразование от левой и правой частей (53) получаем:
![]()
Тогда системная функция трансверсального фильтра будет иметь вид:
![]()
Равенство (54) определяет дробно-рациональную функцию от Z . Она имеет L-кратный полюс при Z=0 и L нулей, определяемых корнями полинома числителя формулы (54). Последние зависят от отсчетов импульсной характеристики ЦФ g(ℓ)=aℓ. Частотная характеристика трансверсального цифрового фильтр согласно (54) и (51) имеет вид:
![]()
Рассмотрим теперь работу ЦФ, работающего по общему алгоритму (52).
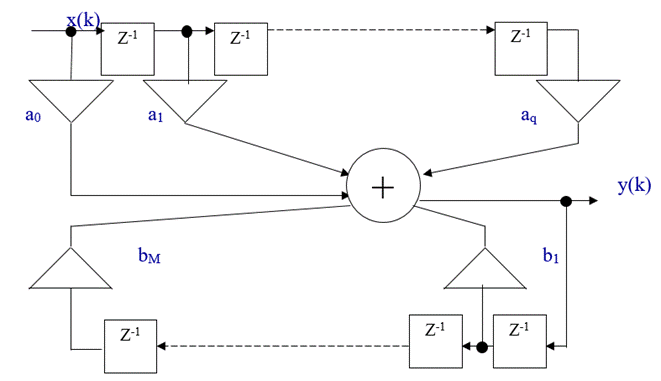
Структурная схема построения рекурсивного ЦФ.
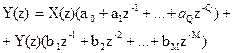
Взяв Z-преобразование от левой и правой частей (52) получим:

Отсюда следует выражение для системной функции цифрового рекурсивного фильтра:
В реализуемых цифровых фильтрах обычно M>Q. При таких условиях дробно-рациональная функция (56) имеет на Z-плоскости: L нулей, определяемых корнями Zoi уравнения:
M-L-кратный ноль в точке Z=0;
![]()
![]()
Если коэффициенты bℓ (ℓ=1,M) вещественны, то корни уравнения (57) (т.е полюса H(z)) лежат либо на вещественной оси, либо образуют комплексно сопряженные пары.
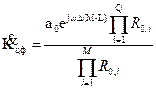
Системной функции (56) соответствует частотная характеристика ЦФ:
где Ro,i=ejwD-zo,i,Rп,i= ejwD- zo,i
АЧХ фильтра (в децибелах) определяется формулой:
За счет наличия обратной связи рекурсивные ЦФ характеризуются нефинитной (длящейся неограниченно) импульсной характеристикой (откликом на единичный импульс (1,0,0,0,…)).
![]()
Система с обратной связью нуждается в исследовании на устойчивость. ЦФ устойчив, если │yn│при n→∞ не превышает некоторого положительного числа А, независимо от выбора начальных условий в схеме. Чтобы исследовать устойчивость схемы, надо исследовать поведение свободных колебаний, т.е. уравнение (52) при отсутствии внешнего воздействия:
![]()
![]()
Известно, что
отдельное свободное колебание в линейной стационарной системе определяется
выражением. При t=kΔ, имеем . Обозначив ![]() решение уравнения
(58) можно искать в виде:
решение уравнения
(58) можно искать в виде:
![]()
Подставляя (59) в (58) получаем характеристическое уравнение, определяющее λ.
![]()
При найденных корнях уравнения (60) или (57) λk=zk, k=1,M, общее решение уравнения (58) можно представить в виде:
где ограниченные коэффициенты А1, А2, …Аm определяются начальными условиями.
![]()
Для момента времен с номером (k+1) из (61) следует:
![]()
Если все полюса системной функции (56) удовлетворяют условию
т.е. они лежат внутри единичного круг с центром в точке z=0, то на основании (61) и (62) можно прийти к заключению, что все свободные колебания во времени определяются членами бесконечно убывающей геометрической прогрессии и фильтр будет устойчивым.
Недостатком рассмотренной схемы рекурсивного ЦФ является наличие отдельных элементов задержки для входных и выходных отсчетов.
Этоn недостаток устранен в так называемой канонической схеме рекурсивного ЦФ, использующего общие элементы задержки для входных и выходных отсчетов, при M=L
![]()
![]() a0
a0
 |
![]()
![]() a1
a1
 |
![]()
![]() a2
a2
 |
|||
 |
|||
![]()
![]()
![]()
![]()
![]()
![]()
![]() x(k)
aL
x(k)
aL
![]()
![]()
![]()

![]()
![]()
![]()
![]() b1
b1
![]()
![]() b2
b2
bM ![]()
![]()
![]()
![]()
![]()
Каноническая схема реализации рекурсивного ЦФ
![]()
Каноническая схема идентична ранее рассмотренной схеме рекурсивного ЦФ. Чтобы это доказать, определим системную функцию ЦФ по канонической схеме. Обозначим значения дискретного отсчета в k-й момент времени на выходе первого сумматора через W(k). Согласно схеме, очевидна справедливость уравнения
![]()
Дискретный сигнал на выходе второго сумматора в k-й момент времени
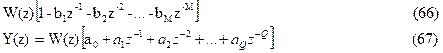
Выполним Z-преобразование над правой и левой частями (64-65). Получим:
Приравняв значения W(z) из (66) и (67), имеем
![]()
Полученный результат не отличается от (56), что доказывает идентичность полной и канонической схем рекурсивного ЦФ.
Синтез цифровых фильтров.
Большое практическое значение имеют методы синтеза ЦФ с требуемым видом импульсной или частотной характеристик ЦФ. Рассмотрим некоторые приемы синтеза ЦФ по заданным характеристикам их аналоговых прототипов.
1) Синтез по заданной импульсной характеристики аналогового прототипа g(t).
ЦФ строится с импульсной характеристикой, которая является результатом дискретизации g(t), т.е. ее k-й отсчет g(k)=g(kΔ). Если в импульсной характеристике Цф ограничится конечным числом слагаемых, получаем реализацию в виде трансверсального фильтра. При неограниченном числе компонент g(k) следует реализация в виде рекурсивного фильтра.
2) Синтез ЦФ по заданной частотной характеристике ќ(ω) (или операторного коэффициента передачи K(p)).
Принципиально нельзя создать ЦФ, частотная характеристики которого ќцф(ω) повторяла бы частотную характеристику аналогового прототипа ќ(ωа), т.к. ќцф(ω) является периодической функцией частоты дискретизации ωg. Однако, можно потребовать, чтобы весь интервал частот ωа, характеризующий аналоговую цепь, был преобразован в отрезок частот ωц ЦФ, на котором сохраняется форма характеристики ќ(ωа), причем
Если для перехода от р-плоскости (отображающей аналоговый прототип) к z-плоскости (отображающей цифровой фильтр) воспользоваться соотношением
![]()
то формально мы от частотной характеристики аналогового
эквивалента переходим к системной функции ЦФ. Однако, если ![]() подставить в выражения для передаточной функции аналогового
прототипа ќ(р), которая для цепей с сосредоточенными параметрами представляет
собой отношение двух полиномов от Р (дробно-рациональную функцию), получим
физически нереализуемую системную функцию ЦФ, т.к. она не выражается отношение
двух полиномов от z.
подставить в выражения для передаточной функции аналогового
прототипа ќ(р), которая для цепей с сосредоточенными параметрами представляет
собой отношение двух полиномов от Р (дробно-рациональную функцию), получим
физически нереализуемую системную функцию ЦФ, т.к. она не выражается отношение
двух полиномов от z.
Надо найти такое преобразование Р в Z, которое привело бы к реализуемому фильтру, но вместе с тем сохраняло бы основное свойство преобразование (69): т.е. переводило бы точки мнимой оси на плоскости Р (точки jω) в точки единичной окружности в z-плоскости.
Для синтеза ЦФ получило широкое распространение билинейное преобразование:
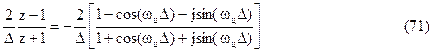 |
![]()
Воспользовавшись формулами ,(71) можно представить так:
Последнему соотношению, согласно (70) соответствует мнимая аналоговая часть вида jωа, следовательно,
При выполнении неравенства следует, что:
В более общем случае надо учесть изменение масштаба по оси частот ЦФ.
Выводы.
1. Устройства ЦОС обладают рядом преимуществ перед устройствами обработки сигналов в непрерывном времени и широко применяются на практике в системах передачи как дискретных, так и непрерывных сообщений.
2. Наиболее широко применяются в системах связи линейные стационарные фильтры и перемножители.
3. Спектр Фурье дискретного сигнала является периодической функцией частоты дискретизации.
4. Линейчатый спектр дискретного (периодического) сигнала с числом отсчетов N определяется дискретным преобразованием Фурье (ДПФ). Число компонент такого спектра Ćn равно N, а число амплитуд – N/2. По спектральным компонентам Ćn дискретные отсчеты x(k) определяются через ОДПФ.
5. Существует методы быстрого преобразования Фурье, позволяющие существенно сократить число операций, выполняемых при расчете ЦФ спектральными методами.
6. При анализе и синтезе ЦФ широко используется
Z-преобразование для получения спектральных характеристик входного и выходного сигналов, и самого цифрового фильтра (его системной функции H(z)). Обратным Z-преобразованием определяются временные характеристики входных и выходных сигналов, а также ЦФ.
7. Частотный коэффициент передачи ЦФ определяется системной функцией фильтра при z=ejwD.
8. Линейные стационарные цифровые фильтры с финитной импульсной характеристикой реализуются трансверсальной схемой, а с неограниченной импульсной характеристикой – рекурсивной схемой (с обратной связью с выхода на вход).
9. Рекурсивные цифровые фильтры устойчивы, если все корни полинома знаменателя системной функции H(z) лежат внутри единичного круга с центром в начале координат.
10. ЦФ часто строятся по аналоговому эквиваленту. Находят применение методы синтеза ЦФ по заданной импульсной характеристике аналогового эквивалента, по заданному дифференциальному уравнению аналогового эквивалента, по заданной частотной характеристике аналогового эквивалента.
11. Выходной шум ЦФ, обусловленный квантованием, тем меньше, чем быстрее убывают отсчеты импульсной характеристики.
12. Выходной шум цифрового перемножителя зависит как от значений отсчетов перемножаемых сигналов, так и от их цифровых компонент.
Рекомендуемая литература
1. Ширман Я. Д. Разрешение и сжатие сигналов. М., «Сов. радио», 1974.
2. Голд Б., Рэйдер Ч. Цифровая обработка сигналов. М., «Сов. радио», 1973.
3. Андреев В. С. Теория нелинейных электрических цепей. М., «Связь», 1972.
Контрольные задания для СРС (тема 15) [1,2,9,10]