Тема 11. Генерирование колебаний  в электрических цепях

 

 

План лекции

1. Автоколебательная система - устройство с ОС.

2. Анализ стационарного режима автогенератора методом гармонической линеаризации

3. Анализ автоколебаний методом уравнений состояния

 

В цепях, содержащих обратные связи, могут возникнуть изменяющиеся во времени электрические токи без воздействия на эти цепи внешних управляющих сигналов. Такие цепи называют автоколебательными системами, а колебания - автоколебаниями.

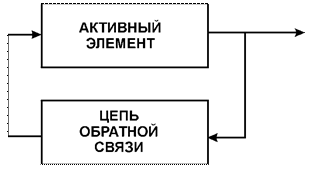
Типичная структура автоколебательной системы - это структура с обратной связью, в которой часть выходного сигнала возвращается на вход через цепь обратной связи.

В наиболее общем случае колебательная система включает источник питания, энергия которого, в конечном случае, и преобразуется в энергию колебаний, цепь управления этим преобразованием, избирательную цепь, служащую для отфильтровывания нужных колебаний, и цепь обратной связи. При анализе таких систем, как правило, источник питания рассматривают как составную часть управляющей цепи (активный управляющий элемент, например, усилитель), а избирательную цепь как составную часть либо активного элемента (колебательный контур в составе резонансного усилителя), либо цепи обратной связи (RC - автогенератором гармонических колебаний, мультивибратора и т.д.). Таким образом анализ колебательной системы сводится к анализу активной цепи с обратной связью (см. рис.).

 

 

С электротехнической точки зрения активный элемент колебательной системы является нелинейным четырехполюсником, коэффициент передачи которого зависит от действующих в его цепях токов и напряжений, а цепь обратной связи - линейным четырехполюсником. Эти свойства элементов системы определяют ее принцип действия.

Действительно, при соответствующем выборе параметров система с обратной связью становится неустойчивой. При этом малые амплитуды любых колебаний, существующих в системе, например, тепловых или коммутационных колебаний, начинают возрастать. С ростом амплитуды коэффициент передачи активного элемента, как правило, уменьшается, и при некотором его значении нарастание амплитуды колебаний прекращается. Установившиеся значение называется стационарным.

При анализе и расчете автоколебательных систем - автогенераторов решают две основные задачи:

1. определение условий при которых, устройство с обратной связью становится неустойчивым, т.е. самовозбуждаются;

2. определение амплитуды и частоты автоколебаний в стационарном режиме.

 

Наиболее сложной является вторая задача, в которой исследуется нелинейная система с обратной связью в режиме больших амплитуд, когда нелинейностью пренебречь нельзя. Первую же задачу решить относительно несложно, поскольку при малых амплитудах автоколебания на начальном этапе процесса нелинейный активный элемент может быть эквивалентно заменен линейной схемой замещения, такой как, например,  у обычного линейного усилителя с ОС. Некоторые сведения об условиях самовозбуждения можно получить даже в общем случае, не рассматривая конкретной схемы автогенератора.

Действительно, коэффициент передачи по напряжению линейного четырехполюсника, охваченного обратной связью, определяется формулой:

 

где - коэффициент передачи активного элемента автогенератора, а  - коэффициент передачи по цепи обратной связи.

В соответствии с алгебраическим критерием устойчивости система становится неустойчивой когда петлевой коэффициент передачи:

 

       (1)

 

В силу комплексности величины, входящих в (1), это соотношение разлагается на два условия:

- условие баланса амплитуд

 

      (2)

 

- и условие баланса фаз

 

       (3).

 

Первое из них свидетельствует о том, что автоколебания в системе возможны, если активный элемент компенсирует все потери энергии в системе, включая нагрузку; второе условие требует, чтобы при этом колебания на входе и выходе петли обратной связи были синфазными.

В общем случае параметры  зависят от частоты. Поэтому условия (2) и (3) обычно выполняются ил только для одной частоты или в достаточно узком диапазоне частот. Чтобы ответить на вопрос “на какой частоте возможны колебания?”, необходимо анализировать конкретную схему.

 

 

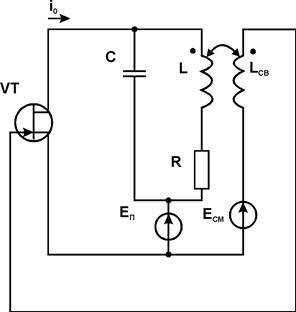
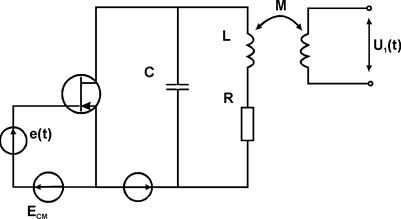
Рассмотрим схему, в которой при определенных условиях могут возникать и существовать автоколебания. Схема содержащая полевой транзистор, колебательный контур и индуктивную цепь обратной связи. Будем считать, что ток стока транзистора связан с напряжением затвор-исток нелинейной зависимостью i0=I(UЗИ).

В колебательном контуре уравнения, связывающие ток в емкости iС c током iL записывается в виде системы:

 

 

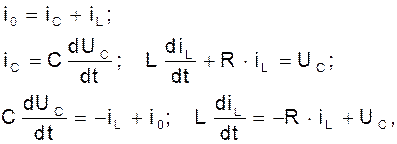
или как одно уравнение

 

 

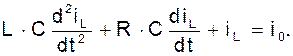
Для цепи обратной связи имеем

 

 

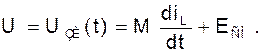
Следовательно, полную систему уравнений цепи можно записать таким образом:

 

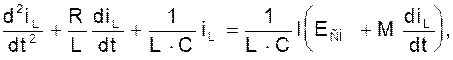   (4)

 

или в развернутом виде:

 

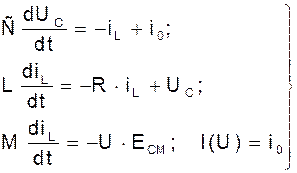      (3)

 

 

 

После включения источников постоянного напряжения в цепи начинается заряд емкости и протекания тока в индуктивности, причем начальные значения iL(t) и UC(t) весьма малы. Напряжение U(t) при этом также будет незначительно отличаться от ЕСМ и зависимость I(U)  может быть существенно упрощена.

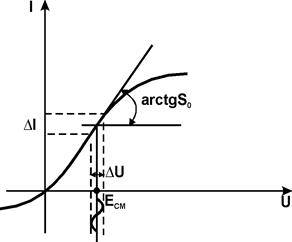
Пусть I(U)=a0+a1U+a2U2+... (см. рис.). Так как

 

 

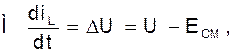
то

 

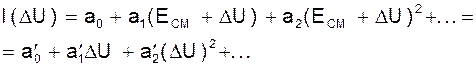
Если принять, что

 

то можно линеаризовать зависимость iC(t)-I(ECM)=a’1DU=S0DU, где S0 - начальная крутизна, равная тангенсу угла наклона касательной к графику I(U) в точке U=EСМ.

Дифференциальное уравнение для тока  будет таким:

 

 

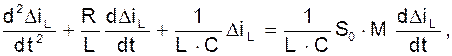
или

 

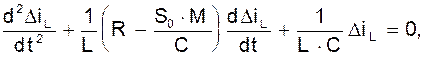  (6).

 

Обозначим 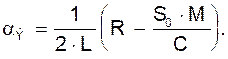 Тогда уравнение (6) можно записать в виде:

 

 

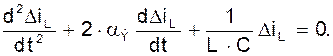
Это линеаризованное уравнение колебательного процесса в автогенераторе на стадии возникновения и нарастания колебаний. Его решения определяет закон суммирования амплитуды колебаний:

 

 

и их частоту

 

 

Начальные значения амплитуды и фазы колебаний можно найти из начальных условий. Но в рассматриваемом случае исходными следует считать случайными флуктуациями токов и напряжений, поэтому особого значения определения их величины не имеет.

Более важным является другое. Если aЭ>0, то какой бы ни была начальная флуктуация тока, процесс в цепи будет затухать. Если же aЭ<0, то сколь угодно малая начальная флуктуация тока будет нарастать с течением времени.

В первом случае цепь является устойчивой. Корни характеристического уравнения

 

 

имеют отрицательную действительную часть.

Во втором случае цепь неустойчива. Неустойчивость может привести к автоколебаниям в цепи. Условием возникновения автоколебаний является положительность действительной части корней характеристического уравнения цепи. Рассмотрим физический смысл условия неустойчивости. Согласно уравнения (6), для возникновения автоколебаний необходимо иметь aЭ<0

Сопротивление потерь в цепи, т.е. превращение энергии колебаний в теплоту, должно быть меньше некоторого значения, обусловленного крутизной характеристики активного элемента и коэффициентом обратной связи. Очевидно, что это условие эквивалентно условию баланса амплитуд вида (2). Фазовое условие существования автоколебаний вида (3) в данном анализе трансформировалось в выражение для частоты колебаний.

Полученное уравнение (6) справедливо только для малых приращений iL(t). Поэтому решение в виде растущей экспоненты справедливо для цепи только на начальном этапе развития процесса автоколебаний. Амплитуда этих колебаний будет возрастать не бесконечно, а достигнет некоторого стационарного значения. Для расчета стационарной амплитуды и частоты колебаний в установившемся режиме используют другой метод, называемый гармонической линеаризацией.

В методе гармонической линеаризации нелинейный резистивный четырехполюсник, включая и избирательный фильтр, заменяется некоторым эквивалентным линейным четырехполюсником с комплексной частотной характеристикой, зависящей от амплитуды входного сигнала. Рассмотрим, как осуществляется такая замена.

 

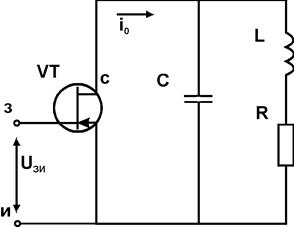
Пусть имеется цепь, состоящая из полевого транзистора с колебательным контуром, включенным в цепь стока (см. рис.). Как и прежде нелинейная зависимость тока стока от напряжения затвор-исток задается многочленом

 

i0=I(U)= =a0+a1U+a2U2+... .

 

Можно показать (см. след. раздел), что если напряжение затвор-исток гармоническое - UЗИ=U0cos(w0t+j0), то ток истока будет определять гармоники с частотами wi=iw0:

 

 

 

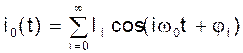
Если колебательный контур настроен на частоту первой гармоники , то на частоте w0 сопротивление контура 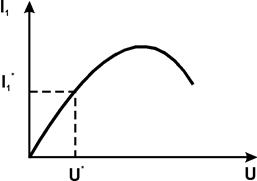. На частотах [(0, 2, 3 ... n) w0], сопротивление контура будет близко нулю. При этом ток в индуктивности  где I1 - амплитуда первой гармоники тока  в нелинейном элементе. В свою очередь, амплитуда тока первой гармоники в нелинейном элементе зависит от вида характеристики этого элемента I(U), т.е. от коэффициентов а1, а3, а5... и т.д., и от амплитуды входного сигнала U. Поэтому

 

I1=I1(а1, а3, а5..., U).

 

Эта зависимость для заданного нелинейного элемента называется колебательной характеристикой. Для нелинейного четырехполюсника описываемого многочленом третьей степени, колебательная характеристика имеет следующий вид: (см. рис.).

Учитывая сказанное и принимая в качестве входного сигнала гармоническое колебание для тока стока бедам иметь:

 

 

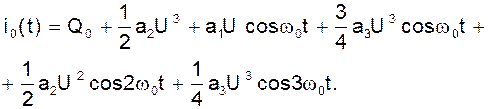
Относительно первой гармоники получаем

 

 

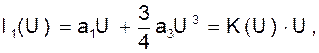
где  - коэффициент передачи (крутизна ВАХ) нелинейного безынерционного элемента на первой гармонике (проводимость).

Таким образом, для каждой конкретной точки U*=const колебательной характеристики (для которой К(U*)=const), зависимость тока первой гармоники от входного напряжения имеет линейный характер I1*=K*U*.

Вернемся к схеме рассматриваемого автогенератора гармонических колебаний. Разомкнем цепь обратной связи и подключим по входу транзистора независимый источник гармонического напряжения e(t) (см. рис.).

 

 

Пусть e(t)=Ucosw0t, . Тогда, согласно методу гармонической линеаризации ток в индуктивности  где j1 - сдвиг фазы между напряжением U1 и током iL. Напряжение   Предположим, что амплитуда этого напряжения равна амплитуде входного напряжения, т.е. , а . Тогда, если мгновенно отключить внешний источник e(t) и замкнуть обратной связи, то колебания в цепи будут продолжаться, как будто бы ничего не изменилось. Это условие стационарного режима: при обходе по петле обратной связи амплитуда остается неизменной, а сдвиг фаз кратен 2p.

Первое условие, как и ранее, является условием баланса амплитуд, второе - условием баланса фаз:

 

           (7)

 

          (8)

 

Здесь K(U) - коэффициент передачи (крутизна ВАХ) безынерционного нелинейного элемента по первой гармонике; KOC(w0) - коэффициент передачи цепи обратной связи; jк - фазовый сдвиг нелинейного элемента, а jОС(w0) - фазовый сдвиг в цепи обратной связи.

Из уравнений (7) и (8) определяется стационарная амплитуда U и стационарная частота w0 колебаний. Для рассматриваемой цепи имеем:

 

 

 

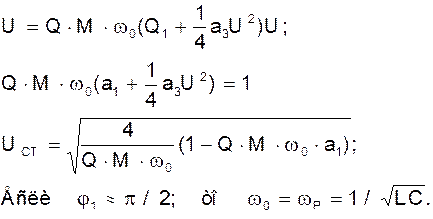
Анализ автоколебаний методом уравнений состояния:

Уравнение (4), получение для автоколебательной цепи, эквивалентно системе уравнений первого порядка:

 

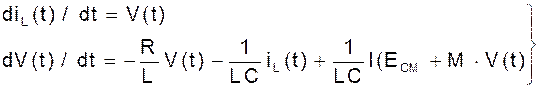(9)

 

Такое представление уравнений цепи соответствует уравнениям состояния.

В силу нелинейного характера функции I(U) найти решение (9) аналитически нельзя. Для анализа процессов применяют численные методы интегрирования систем дифференциальных уравнений - численное моделирование.

Простейший подход состоит в приближенной замене производной от функции f(t):

 

 

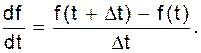
Обозначим  получим

 

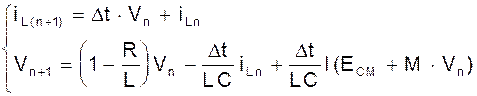(10)

 

Предположим, что известна начальная флуктуация iL(0)=i0; V(0)=0. Поскольку функция I(U) может быть вычислена для любых значений аргумента, подставляя в (10), получаем:

 

 

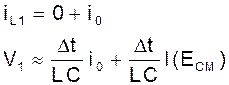
Теперь, подставив полученные значения снова в (10), найдем iL2, V2 и т.д. Этот метод приближенного решения носит название метода Эйлера.

 

Рекомендуемая литература

1.     Карни Ш. Теории цепей. Анализ и синтез. М., «Связь», 1973.

2.     Френкс Л. Теория сигналов. М., «Сов. радио», 1974.

3.       Тихонов В. И. Статистическая радиотехника. М., «Сов. радио», 1966.

 

Контрольные задания для СРС (тема 11) [1,2,9,10]