Тема 6. Радиосигналы и классификация
методов модуляции.
План лекции
1. Общие определения
2. Классификация методов модуляции
Для передачи
информации на расстояние применяются сигналы, эффективно излучаемые с помощью
антенных устройств, обладающие
способностью распространяться в виде свободных радиоволн в среде, разделяющей отправителя и получателя
информации. Такими сигналами являются высокочастотные
колебания. Передаваемая информация
должна быть тем или иным способом
заложена в высокочастотное колебание, называемое несущим. Частота 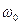 этого
колебания выбирается в зависимости от расстояния, на которое должна передаваться информация, от условий распространения радиоволн и ряда других
технических и экономических
факторов. Но в любом случае частота
этого
колебания выбирается в зависимости от расстояния, на которое должна передаваться информация, от условий распространения радиоволн и ряда других
технических и экономических
факторов. Но в любом случае частота 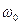 должна
быть велика по сравнению с наивысшей частотой спектра передаваемого сообщения.
должна
быть велика по сравнению с наивысшей частотой спектра передаваемого сообщения.
Это объясняется тем, что для неискаженной передачи сообщения
через радиотехнические цепи, а также для устранения искажений,
обусловленных распространением радиоволн, необходимо, чтобы ширина
спектра сообщения 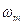 была мала по
сравнению
была мала по
сравнению 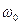 ; чем меньше
отношение
; чем меньше
отношение 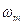 /
/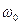 , тем меньше проявляется несовершенство характеристик
системы. Поэтому чем выше требуемая скорость передачи информации, и, следовательно, шире спектр
сообщения
, тем меньше проявляется несовершенство характеристик
системы. Поэтому чем выше требуемая скорость передачи информации, и, следовательно, шире спектр
сообщения 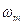 , тем выше должна быть несущая частота
радиосигнала. Как правило, выполняется
неравенство
, тем выше должна быть несущая частота
радиосигнала. Как правило, выполняется
неравенство 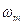 /
/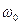 <<1.
<<1.
Любой радиосигнал можно поэтому трактовать как «узкополосный» процесс
даже при передаче «широкополосных» сообщений.
Приведем следующие примеры. При передаче
речи или музыки спектр
сообщения обычно ограничивают полосой от Fmin = 30-50Гц до Fмакс = 3000—10 000 Гц.
Даже на самой длинной волне вещательного
диапазона 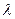 = 2000
м пои несущей частоте f0 =150 кГц, отношение Fмакс/f0 < 104/f0*1,5 • 105 = 0,06. При передаче тех же сообщений на коротких волнах (при
частотах 15-20 МГц) это отношение не
превышает сотых долей процента. При передаче подвижных изображений
(телевидение) полоса частот сообщения
весьма широка и достигает 5—6 МГц, однако и несущая частота выбирается
не менее 50—60 МГц, так что отношение Fmax/f0 не превышает 10%.
= 2000
м пои несущей частоте f0 =150 кГц, отношение Fмакс/f0 < 104/f0*1,5 • 105 = 0,06. При передаче тех же сообщений на коротких волнах (при
частотах 15-20 МГц) это отношение не
превышает сотых долей процента. При передаче подвижных изображений
(телевидение) полоса частот сообщения
весьма широка и достигает 5—6 МГц, однако и несущая частота выбирается
не менее 50—60 МГц, так что отношение Fmax/f0 не превышает 10%.
В самом общем случае радиосигнал, несущий в
себе информацию, можно
представить в виде
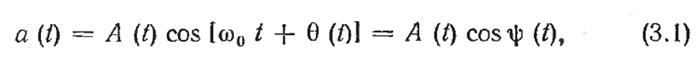
в
котором амплитуда А или фаза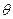 изменяются по
закону передаваемого
сообщения.
изменяются по
закону передаваемого
сообщения.
Если А и 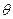 — постоянные
величины, то выражение (3.1) описывает простое гармоническое колебание, не
содержащее в себе никакой информации. Если А и
— постоянные
величины, то выражение (3.1) описывает простое гармоническое колебание, не
содержащее в себе никакой информации. Если А и 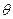 (следовательно, и
(следовательно, и 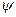 ) подвергаются принудительному
изменению для передачи сообщения, то колебание становится модулированным.
) подвергаются принудительному
изменению для передачи сообщения, то колебание становится модулированным.
В зависимости от того, какой из двух параметров
изменяется — амплитуда А или угол 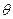 — различают два
основных вида модуляции: амплитудную и угловую. Угловая модуляция, в свою
очередь, подразделяется на
два вида: частотную (ЧМ) и фазовую (ФМ). Эти
два вида модуляции между собой тесно связаны, и различие между ними проявляется лишь в характере изменения
во времени угла
— различают два
основных вида модуляции: амплитудную и угловую. Угловая модуляция, в свою
очередь, подразделяется на
два вида: частотную (ЧМ) и фазовую (ФМ). Эти
два вида модуляции между собой тесно связаны, и различие между ними проявляется лишь в характере изменения
во времени угла 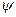 при одной и той же
модулирующей функции.
при одной и той же
модулирующей функции.
Модулированное колебание имеет спектр, структура
которого зависит как от спектра передаваемого сообщения, так и от вида модуляции. То
обстоятельство, что ширина спектра модулирующего сообщения мала по сравнению с
несущей частотой 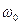 , позволяет считать
A (t) и
, позволяет считать
A (t) и 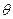 (t) медленными функциями времени.
Это означает,
что относительные изменения A (t) и
(t) медленными функциями времени.
Это означает,
что относительные изменения A (t) и 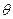 (t) за один период несущего колебания
малы по сравнению с единицей.
(t) за один период несущего колебания
малы по сравнению с единицей.
Рассмотрим сначала вопрос об изменении
амплитуды. При скорости изменения амплитуды dAldt приращение
амплитуды за один период Т0
можно приближенно приравнять (dAldt) T0. Следовательно, относительное изменение за период равно
Можно считать,
что условие медленности функции А(t) выполняется, если
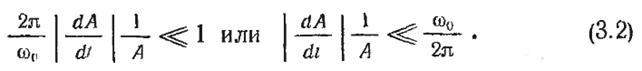
Аналогичным образом можно установить
условие медленности функции 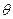 .
.
Так как мгновенная частота колебания
равна скорости изменения фазы, то, дифференцируя аргумент выражения (3.1),
находим
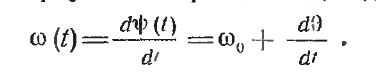
Производная 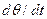 определяет отклонение частоты
определяет отклонение частоты 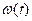 от частоты
от частоты 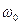 . Это отклонение может быть
быстрым или медленным. Для того чтобы колебание а(t) можно было считать близким
к гармоническому, нужно потребовать, чтобы изменение частоты за один цикл
. Это отклонение может быть
быстрым или медленным. Для того чтобы колебание а(t) можно было считать близким
к гармоническому, нужно потребовать, чтобы изменение частоты за один цикл 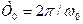 было мало по сравнению с
частотой
было мало по сравнению с
частотой 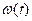 в
рассматриваемый момент времени.
в
рассматриваемый момент времени.
Таким образом, условие медленности
функции 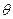 (t) можно
записать в виде следующего неравенства:
(t) можно
записать в виде следующего неравенства:
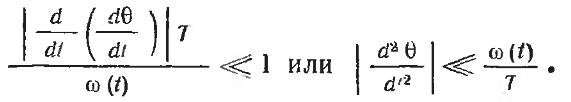
Так как обычно 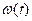 очень мало отличается от
очень мало отличается от 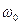 , можно исходить из условия
, можно исходить из условия

Для большинства используемых в
радиотехнике сигналов неравенства (3.2) и (3.3) обычно выполняются. Это
означает, что при любом виде модуляции параметры радиосигнала: амплитуда, фаза
и частота – изменяются настолько медленно, что в пределах одного периода
колебание можно считать гармоническим.
Исследование видов модуляции необходимо
для определения свойств каналов, сокращения избыточности модулированных
сигналов и улучшения использования мощности передатчиков, определения
потенциальной помехоустойчивости, помех соседним каналам и успешного решения
проблем электромагнитной совместимости радиосистем ; разработки оптимальных
методов реализации.
Идеальная непрерывная модуляция - это перенос
спектра полезного сигнала в область более высоких частот без нелинейных,
частотных и фазовых искажений. Если полезный сигнал представить в виде
узкополосного процесса
U(t)=A(t)cos[w0t+Ф(t)], (1)
то в идеальном случае модулированный
сигнал
S(t)=A(t)cos[w1t+Ф(t)], (2)
где w1=w0+w2 - средняя частота сигнала-переносчика.
Из (1) и (2) следует, что при идеальной
модуляции законы распределения огибающей и фазы узкополосного сигнала не должны
изменяться, изменяется только средняя частота. Корреляционная функция огибающей
не изменяется, а частота “косинусоидального заполнения” корреляционной функции
модулированного сигнала равна w1. Спектр модулированного сигнала
смещается в область средней частоты w1, но
не изменяет своей формы. Реально модуляция сопровождается нелинейными,
частотными и фазовыми искажениями. Поэтому, как правило, ширина спектра
модулированных сигналов больше ширины спектра полезных сигналов, искажаются
законы распределения огибающей и фазы, изменяются формы корреляционных функций
и спектральных плотностей. Если полезный сигнал - случайный стационарный
процесс, а сигнал - переносник - гармоническое колебание, то модулированный
сигнал будет нестационарным случайным процессом, корреляционная функция и
спектральная плотность которогозависят от текущего момента времени.
Для определения средних спектральных и
корреляционных характеристик модулированного сигнала необходимо применять
операцию усреднения но необходимо применять операцию усреднения по времени. В
этом более общем случае соотношения Хинчина - Винера принимают вид
S1(w)=2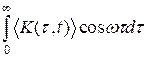 (3)
(3)
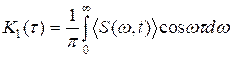 , (4)
, (4)
где S1(w), K1(t) - средняя спектральная плотность и средняя корреляционная
функция модулированного сигнала.
Корреляционные функции, спектральные
плотности, законы распределения огибающей и фазы модулированных сигналов
получают по заданным оператором модуляции, корреляционным функциям или
спектральным плотностям, законам распределения огибающих и фаз полезного
сигнала и переносчика.
Для классификации видов модуляции удобно
использовать следующие признаки : характер полезного сигнала и переносчика (
детерминированный процесс, случайный стационарный процесс, случайный
нестационарный процесс); сигналов (аналоговые, дискретные); информационного
параметра (амплитуда, частота, фаза, длительность, период и т.д.) и др. В
простейшем случае учитывают всего два признака : модулирующего сигнала и
переносчика. Условно введем следующие классы модулирующих сигналов U(t)
:
А - детерминированные непрерывнозначные
процессы;
В - детерминированные дискретные
последовательности;
С - случайные стационарные
непрерывнозначные процессы;
D - случайные стационарные
последовательности;
Е - случайные нестационарные
непрерывнозначные процессы;
F - случайные нестационарные
последовательности;
G - дискретные случайные стационарные
последовательности;
H - дискретные случайные нестационарные
последовательности
(см. ГОСТ 2187 - 76).
Аналогично введем классы переносчиков X(t)
и для удобства записи обозначим их цифрами 1 - 8. В соответствии с введенными
обозначениями класс А1 включает все непрерывные виды модуляции, в которых
полезные сигналы и переносчики являются детерминированными непрерывными
процессами; класс В1 - все виды модуляции, в которых каждый сигнал
рассматривают как детерминированную импульсную последовательность, а переносчик
- как детерминированный непрерывный сигнал.
Аналогично объединяют в классы остальные
виды модуляции. В теории передачи информации и передачи сигналов основное
внимание уделяют тем классам модуляции, в которых полезные сигналы
рассматривают как случайные. Это обусловлено тем, что детерминированные сигналы
не несут информации. Далее, в процессе составления описания, рассматривают
корреляционные и спектральные характеристики модулированных случайных сигналов.
Рекомендуемая литература
1.
Ширман Я. Д.
Разрешение и сжатие сигналов. М., «Сов. радио», 1974.
2.
Голд Б., Рэйдер Ч.
Цифровая обработка сигналов. М., «Сов. радио», 1973.
3.
Андреев В. С.
Теория нелинейных электрических цепей. М., «Связь», 1972.
Контрольные задания для СРС (тема 6)
[1,2,9,10]
![]() этого
колебания выбирается в зависимости от расстояния, на которое должна передаваться информация, от условий распространения радиоволн и ряда других
технических и экономических
факторов. Но в любом случае частота
этого
колебания выбирается в зависимости от расстояния, на которое должна передаваться информация, от условий распространения радиоволн и ряда других
технических и экономических
факторов. Но в любом случае частота ![]() должна
быть велика по сравнению с наивысшей частотой спектра передаваемого сообщения.
должна
быть велика по сравнению с наивысшей частотой спектра передаваемого сообщения.![]() была мала по
сравнению
была мала по
сравнению ![]() ; чем меньше
отношение
; чем меньше
отношение ![]() /
/![]() , тем меньше проявляется несовершенство характеристик
системы. Поэтому чем выше требуемая скорость передачи информации, и, следовательно, шире спектр
сообщения
, тем меньше проявляется несовершенство характеристик
системы. Поэтому чем выше требуемая скорость передачи информации, и, следовательно, шире спектр
сообщения ![]() , тем выше должна быть несущая частота
радиосигнала. Как правило, выполняется
неравенство
, тем выше должна быть несущая частота
радиосигнала. Как правило, выполняется
неравенство ![]() /
/![]() <<1.
<<1.![]() = 2000
м пои несущей частоте f0 =150 кГц, отношение Fмакс/f0 < 104/f0*1,5 • 105 = 0,06. При передаче тех же сообщений на коротких волнах (при
частотах 15-20 МГц) это отношение не
превышает сотых долей процента. При передаче подвижных изображений
(телевидение) полоса частот сообщения
весьма широка и достигает 5—6 МГц, однако и несущая частота выбирается
не менее 50—60 МГц, так что отношение Fmax/f0 не превышает 10%.
= 2000
м пои несущей частоте f0 =150 кГц, отношение Fмакс/f0 < 104/f0*1,5 • 105 = 0,06. При передаче тех же сообщений на коротких волнах (при
частотах 15-20 МГц) это отношение не
превышает сотых долей процента. При передаче подвижных изображений
(телевидение) полоса частот сообщения
весьма широка и достигает 5—6 МГц, однако и несущая частота выбирается
не менее 50—60 МГц, так что отношение Fmax/f0 не превышает 10%.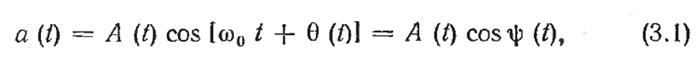
![]() изменяются по
закону передаваемого
сообщения.
изменяются по
закону передаваемого
сообщения.![]() — постоянные
величины, то выражение (3.1) описывает простое гармоническое колебание, не
содержащее в себе никакой информации. Если А и
— постоянные
величины, то выражение (3.1) описывает простое гармоническое колебание, не
содержащее в себе никакой информации. Если А и ![]() (следовательно, и
(следовательно, и ![]() ) подвергаются принудительному
изменению для передачи сообщения, то колебание становится модулированным.
) подвергаются принудительному
изменению для передачи сообщения, то колебание становится модулированным.![]() — различают два
основных вида модуляции: амплитудную и угловую. Угловая модуляция, в свою
очередь, подразделяется на
два вида: частотную (ЧМ) и фазовую (ФМ). Эти
два вида модуляции между собой тесно связаны, и различие между ними проявляется лишь в характере изменения
во времени угла
— различают два
основных вида модуляции: амплитудную и угловую. Угловая модуляция, в свою
очередь, подразделяется на
два вида: частотную (ЧМ) и фазовую (ФМ). Эти
два вида модуляции между собой тесно связаны, и различие между ними проявляется лишь в характере изменения
во времени угла ![]() при одной и той же
модулирующей функции.
при одной и той же
модулирующей функции.![]() , позволяет считать
A (t) и
, позволяет считать
A (t) и ![]() (t) медленными функциями времени.
Это означает,
что относительные изменения A (t) и
(t) медленными функциями времени.
Это означает,
что относительные изменения A (t) и ![]() (t) за один период несущего колебания
малы по сравнению с единицей.
(t) за один период несущего колебания
малы по сравнению с единицей.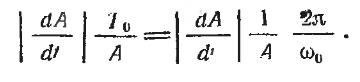
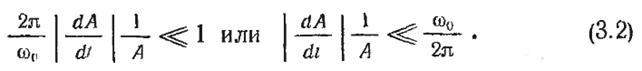
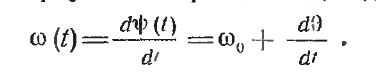
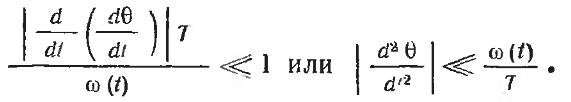

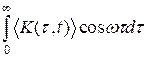 (3)
(3)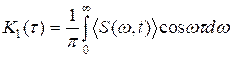 , (4)
, (4)