Тема 2. Ортогональные разложения Котельникова для непрерывных сигналов.

План лекции

1. Сигналы с ограниченными и полосовыми спектрами.

2. Сигналы с полосовыми спектрами.

3. Теорема отсчетов в частотной области.

С целью упрощения задач анализа сигналов в инженерных расчетах учитывают только ту часть спектра, в которой сосредоточено до 80...95% энергии сигнала. Поэтому чаще всего большинство сигналов рассматривают как сигналы с ограниченными спектрами. Для их анализа наряду с разложением Фурье широко применяют разложение Котельникова.

Рассмотрим основные особенности этого разложения.

Ортогональное разложение Котельникова для непрерывных сигналов с ограниченными спектрами позволяет представлять их в виде импульсных последовательностей (см. рис.) Теоретической основой разложения служит теорема Котельникова (теорема отсчетов): любая непрерывная функция S(t), не содержащая частот выше F, полностью определяется последовательностью значений в моменты, отстоящие друг от друга на время Dt=1/2F.

Общее число отсчетов n для сигнала длительностью Т будет равно n=T/Dt=2FT=n. Число n называют базой сигнала.

Для сигнала S(t), спектр которого лежит в интервале [0,F], ортогональное разложение Котельникова имеет вид

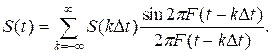                                                                                                           (44)

где S(kDt)=S_k - отсчет сигнала в момент времени t_k ;                

[sin2pF(t-kDt)]/[2pF(t-kDt)] - базисная система ортогональных функций с общей нормой 1/2F;

Dt=1/2F-интервал дискретизации, равный норме базисных функций.

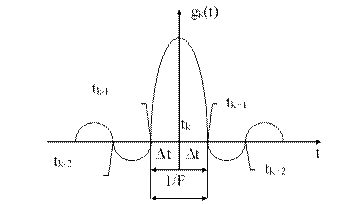
Функция g_k=[sin2pF(t-kDt)]/[2pF(t-kDt)]  называют функциями отсчетов, а значения S(kDt) - отсчетами. График функции отсчетов имеет следующий вид (см. рис.).

Ортогональность функций отсчетов проверяют путем вычисления интеграла

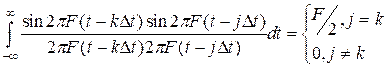
Интервал дискретизации не превышает половины периода наиболее высокой частоты спектра сигнала, что уменьшает число членов в данном разложении по сравнению с разложением Фурье при одинаковой точности аппроксимации. Точность аппроксимации так же как и в случае разложения Фурье определяется равенством (12). При этом мощность сигнала, через заданную последовательность временных выборок, выражается равенством Парсеваля (формула (8)):

 - энергия сигнала

Е=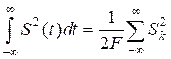                                                                                                       (45)

- мощность сигнала за период колебания

P=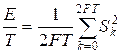.                                                                                                             (46)   

Из последнего выражения следует, что средняя за период Т мощность непрерывного сигнала равна среднему квадрату выборки. Усреднение производится по всем интервалам, число которых 2FT.

Достоинства ортогонального разложения Котельникова следующие: базисная система ортогональных функций выбрана так, что ряд (44) носит формальный характер, т.е. в любой момент отсчета t_k он дает одно значение S_k, остальные составляющие ряда вырождаются в нуль; коэффициенты ряда (44) можно не вычислять; их определяют путем измерения значений сигнала или из его аналитической формы ; зная длительность сигнала Т и граничную частоту F, определяют требуемое число отсчетов n=2FT и энергию сигнала из (45); относительная простота реализации как разложения (т.е. дискретизации) непрерывного сигнала в импульсную последовательность, так и последующего его восстановления.

Остановимся более подробно на последней особенности. Для этого рассмотрим физический смысл разложения Котельникова. Каждый член суммы (44) представляет собой отклик идеального фильтра нижних частот g_k (см. рис.) с частотой среза F на очень короткий импульс, приходящий в момент t_k=kDt и имеющий площадь S(kDt). Поэтому при дискретной передаче сигнала S(t) с ограниченным спектром необходимо через равные интервалы времени Dt брать отсчеты мгновенных значений сигнала и передавать по каналу последовательность достаточно коротких импульсов длительностью t, причем t/Dt<<1. Амплитуду импульсов A_k в момент времени t_k=kDt выбирают так, чтобы A_kt=S(kDt)=S_k. В приемном устройстве выделенная последовательность видеоимпульсов пропускается через фильтр нижних частот, на выходе которого восстанавливается переданный непрерывный сигнал. Длительность импульсов t может быть сколь угодно малой, но выбирают ее исходя из полосы прозрачности канала связи. Частота дискретизации ( тактовая частота ) равна 2F.

Сигналы с полосовыми спектрами. Если сигнал S(t) непрерывный, имеет полосовой спектр с шириной DF₁=f₁-f₂, то его можно представить в виде ортогонального разложения следующего вида:

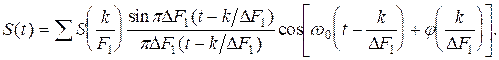                                                                    (46)

где w₀=2p(f₁+f₂)/2 - среднее значение угловой частоты спектра сигнала; Dt=1/2DF₁; S(k/DF₁); j(k/DF₁) - отсчеты амплитуды и фазы сигнала в моменты t_k=kDt. Из формулы видно, что для сигналов с полосовыми спектрами необходимо через интервал дискретизации отсчитывать мгновенные значения не только амплитуд, но и фаз. Так, в частности, дискретизируют однополосные колебания - сигналы с полосовыми спектрами.      

Основные особенности ортогонального разложения Котельникова вида (46) следующие : базисная система включает совокупность ортогональных функций отсчетов, каждая из которых представляет собой модулированное по амплитуде колебание с несущей частотой w₀ и огибающей, определяемой функцией g_k(t); помимо отсчетов амплитуд берутся отсчеты фаз; если длительность сигнала Т, то число отсчетных точек n=T/Dt=2TDF₁.

В целом, все ортогональные разложения Котельникова - теоретическая основа большинства методов дискретной передачи непрерывных сигналов. Они позволяют с единых позиций рассматривать передачу как дискретных, так и непрерывных сигналов.

Теорема отсчетов в частотной области. При анализе сигналов с непрерывными спектрами часто бывает необходимо представить сигнал с помощью частотных выборок спектральной функции , а не временных выборок функции S(t).

Для функции  можно составить ряд, аналогичный выражению (44), на основании взаимной заменяемости переменных t и w в паре преобразований Фурье (36), (37). Применительно к выражению (44) это означает, что t следует заменить на w, 2W=2pF на Т, Dt=1/2F на Dw=2p/T.

Таким образом получаем

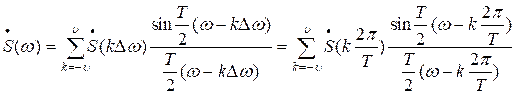                                                            (7)

Расстановка частотных выборок иллюстрируется следующим рисунком.

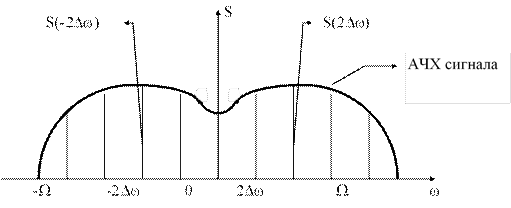
Если ранее временной интервал между двумя соседними выборками не должен был превышать 2p/2W, то теперь частотный интервал не должен превышать 2p/T. При ширине спектра 2W, охватывающей область частот   -W<W<W, число выборок равно 2W/Dw=2FT, т.е. как и при представлении сигнала рядом (44).

В общем случае выборки  являются комплексными числами и в каждой отсчетной точке на оси частот должны быть заданы два параметра - действительная и мнимая части , или модуль и аргумент. Таким образом общее число параметров получается вдвое большим, чем при временном представлении сигнала, когда выборки S(k/2F) - действительные числа. Избыточность представления сигнала в частотной области легко устраняется, если учесть, что  и  являются комплексно-сопряженными функциями, так что задание одной из них однозначно определяет другую. Таким образом, спектр сигнала полностью характеризуется совокупностью комплексных выборок, взятых только в области положительных частот, и число независимых параметров n=2FT, как и при представлении сигнала во временной области.

Рекомендуемая литература

1. Карни Ш. Теории цепей. Анализ и синтез. М., «Связь», 1973.

2. Френкс Л. Теория сигналов. М., «Сов. радио», 1974.

3. Тихонов В. И. Статистическая радиотехника. М., «Сов. радио», 1966.

Контрольные задания для СРС (тема 2) [1,2,9,10]