Тема 1

Тема 1. Предмет, метод и основные задачи РЦиС. Теория сигналов.

План лекции

1. Предмет изучения РЦиС

2. Классификация сигналов

3. Спектральный анализ и синтез детерминированных сигналов

Электрическим сигналом S(t) называют изменение электрического заряда, или тока, или напряжения во времени.

Различают следующие виды сигналов:

1. сигналы, произвольные по величине и непрерывные во времени. Сюда относят аналоговые сигналы (без разрывов) и континуальные сигналы (с разрывами);

2. сигналы произвольные по величине и дискретные во времени (дискретные сигналы);

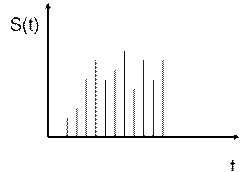
3. сигналы, квантованные по величине и непрерывные во времени (квантованные сигналы);

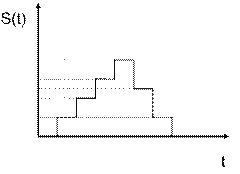
4. сигналы, квантованные по величине и дискретные во времени (цифровые сигналы);

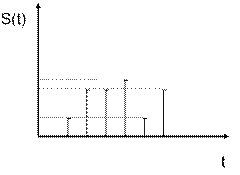
Все четыре разновидности сигналов называются детерминированными, если мгновенное значение сигнала можно заранее предсказать в любой момент времени с вероятностью 1, т.е. абсолютно достоверно. К таким сигналам относятся, в основном, управляющие сигналы и несущие колебания. Если же мгновенное значение сигнала заранее неизвестно и может быть предсказано с вероятностью < 1, то такие сигналы называются случайными. Как правило, все информационные колебания являются случайными. Сюда могут быть отнесены все четыре разновидности сигналов.

К случайным сигналам относят также шумовые колебания, представляющие собой суперпозицию различных случайных сигналов.

Для описания детерминированных сигналов используют амплитудно - временные характеристики и представления в виде суперпозиции простых колебаний.

Для описания случайных сигналов применяют методы теории вероятности и математической статистики; случайные сигналы моделируют детерминированными сигналами.

Изучение теории сигналов обычно начинают с изучения свойств и математических моделей детерминированных сигналов, которые потом дополняют различными статистическими методами.

Амплитудно - временные параметры детерминированных сигналов. Рассмотрим график зависимости напряжения от времени, представляющий собой прямоугольный импульс с различными отклонениями от идеальной формы. На его примере рассмотрим некоторые возможные параметры, используемые для описания различных сигналов в амплитудно - временных координатах.

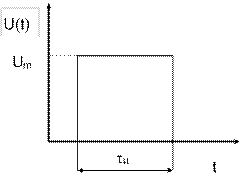
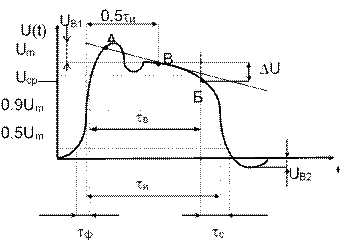
Импульс идеальной формы. Импульс реальной формы.

где U_m- амплитуда импульса;

U_ср- средняя амплитуда импульса;

U_В1- выброс фронта;

U_В2- выброс среза;

DU- скол вершины;

t_и- длительность импульса;

t_ф- длительность фронта;

t_ср- длительность среза;

t_в- длительность вершины;

У сигналов другой формы могут исключаться и добавляться некоторые параметры. Кроме сигналов в виде одиночных импульсов, как здесь рассмотренный, широко применяются периодически повторяемые сигналы. В этом случае к набору рассмотренных параметров добавляется период повторения сигнала Т , или частота повторения F= 1/T или w=2pF.

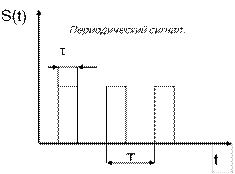
Кроме того часто используется обобщен-

ный параметр периодической последо-

вательности импульсов называемый

скважностью : Q=T/t_и , или коэффици -

ент заполнения, определяемый как

K_зап=1/Q.

Используя упомянутые параметры сигналов, составляют их математические модели. При этом очень широко используется метод кусочной аппроксимации, когда на каждом конкретном отрезке времени t³t₁,t₂ мгновенное значение сигнала , описывают некоторой функцией. В качестве последней широко используется линейная функция U=kt, где k=const. В этом случае метод называют методом кусочно - линейной аппроксимации. Например, математическая модель периодического трансцендального сигнала с помощью этого метода может быть записана следующим образом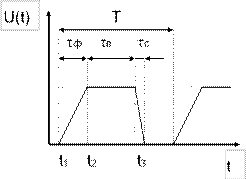

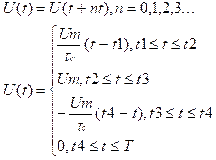
Методы кусочной аппроксимации и другие методы аналитического описания сигналов не решают в полном объеме задач математического моделирования сложных сигналов, и , следовательно, задач прохождения сигналов через различные цепи. В некоторой степени эти проблемы разрешаются с помощью спектральной теории сигналов.

Обобщенной спектральной теорией называют совокупность методов представления сигналов в виде суммы ортогональных составляющих

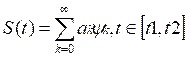(1)

Наибольшее распространение получили методы, использующие представления сигналов в виде колебаний (т.е. функций времени ) и спектрального разложения на синусоидальные и косинусоидальные составляющие ( это преобразования Фурье ). Обобщенная спектральная теория исследует общие закономерности спектрального анализа для систем базисных функций и рассматривает особенности выбора базисных систем при решении задач передачи и обработки сигналов. Представление (1) называют разложением сигнала по системе базисных функций. К системе базисных функций предъявляют следующие требования : для любого сигнала ряд (1) должен сходиться; функции _к(t) должны иметь простую аналитическую форму; коэффициенты а_к должны вычисляться относительно просто. Этим трем условиям удовлетворяют системы ортогональных функций. Условие ортогональности функций

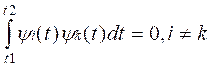(2)

При i=k

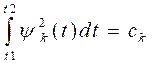(3)

Число c_k называют нормой базисной функции . Нормированная базисная функция

(4)

Система нормированных базисных функций , удовлетворяющая одновременно и условию ортогональности, и условию нормировки

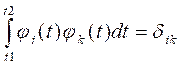(5)

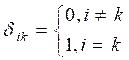
где , называется ортонормированной.

Если под y_i или y_k понимать ток или напряжение, то равенство (3) имеет смысл энергии сигнала, выделенной сигналом y_k на сопротивлении 1 Ом за время (t₂-t₁), а равенство (2) имеет смысл энергии взаимодействия сигналов y_i и y_k. Отсюда следует физический смысл понятий ортогональности и нормы функций: ортогональные сигналы не взаимодействуют между собой, а энергия нормированного сигнала равна 1.

Рассмотрим, как определяют коэффициенты а_к при разложении сигнала по системе ортонормированных функций. Представим сигнал

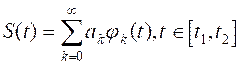(6)

Умножив обе части (6) на j_i(t) и проинтегрировав на интервале [t₁,t₂] получим

(*)

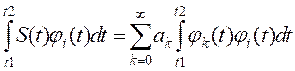Из условия ортонормированности функций (5) следует, что в правой части соотношения (*) все интегралы при i¹k будут равны нулю, а при i=k один из них равен единице. Поскольку знак суммы в правой части (*) при этом исчезает, то

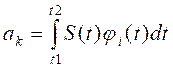(7)

Ортогональные разложения (6) называют обобщенным рядом Фурье, а коэффициенты (7) - обобщенным коэффициентом Фурье.

Ортонормированные функции удовлетворяют трем условиям: они должны иметь простую аналитическую форму; для любого сигнала ряд должен сходиться; коэффициенты a_k должны вычисляться относительно просто.

Выбор базисных ортонормированных функций - одна из ответственных задач и ее решение существенно зависит от характера преобразований сигналов в системе. Коэффициенты a_k представляют собой эффективные значения составляющих спектра (обобщенных гармоник), поэтому выделяемая на сопротивлении 1 Ом средняя мощность сигнала равна:

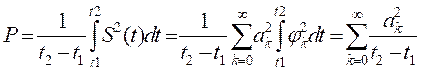(8)

Соотношение (8) называют равенством Парсеваля. Из него следует, что мощность сигнала равна сумме мощностей всех составляющих спектра.

Определим коэффициенты, минимизирующие погрешность ортогонального разложения. Используем для этого понятие среднеквадратичной погрешности :

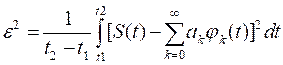(9)

Для минимизации необходимо решить систему уравнений вида

(**)

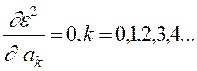Для этого, при условии необходимо найти из решения a_kопт, подставить значения этих коэффициентов в (9) и определить

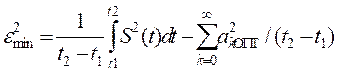(10)

Эту задачу решил Фурье. Он показал, что оптимальными будут коэффициенты, определяемые по соотношению (7) ; если число членов ряда n< , то имеется некоторая среднеквадратическая погрешность , из-за которой

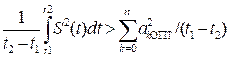и (11)

если же n® , то это неравенство выраждается в равенство Парсеваля (8) и, следовательно, .

Таким образом, бесконечный ряд дает адекватное в среднеквадратическом смысле ортонормированное разложение сигнала.

Рекомендуемая литература

1. Гоноровский И. С. Радиосигналы и переходные явления в радиоцепях, М ., Связьиздат, 1954.

2. Зиновьев А. Л., Филиппов Л. И. Введение в теорию сигналов и цепей, 2-ое Изд., М., «Высшая школа», 1975.

3. Атабеков Р. И. Основы теории цепей. М., «Энергия», 1969.

Контрольные задания для СРС (тема 1) [1,2,3]