Тема 1. Элементы линейной алгебры
Практическое занятие №3
Системы линейных алгебраических уравнений
1. Формулы Крамера
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными
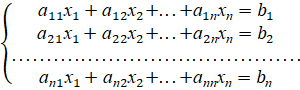
Матрица ![]() , составленная из коэффициентов
системы, называется матрицей системы. Положим
, составленная из коэффициентов
системы, называется матрицей системы. Положим ![]() . Тогда решение системы можно найти
по формулам Крамера:
. Тогда решение системы можно найти
по формулам Крамера:
![]()
![]()
Нетрудно видеть, что ![]() есть определитель, который
получается из определителя матрицы A
заменой i-го столбца столбцом
свободных членов.
есть определитель, который
получается из определителя матрицы A
заменой i-го столбца столбцом
свободных членов.
Пример 1. Найти решение системы уравнений

а) найдем определители:
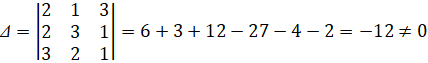
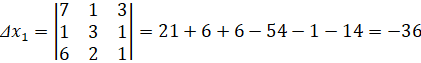
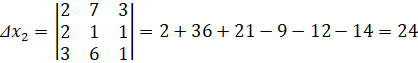
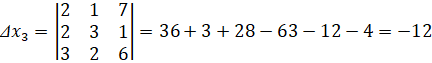
По формулам Крамера получим решение
![]()
![]()
![]()
Пример 2. Найти решение системы уравнений
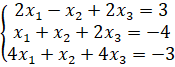
а) найдем определители:
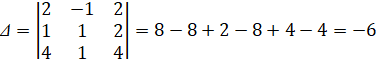
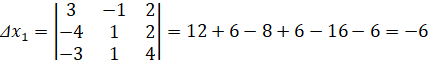
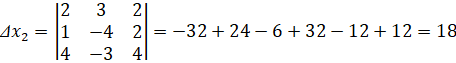
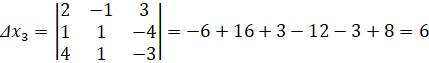
По формулам Крамера получим решение
![]()
![]()
![]()
2. Решение систем матричным способом
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными
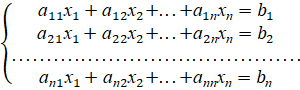
Рассмотрим
матрицу ![]() системы. Положим
системы. Положим ![]() .
.
Введем еще две матрицы: X- матрица-столбец неизвестных; B- матрица-столбец свободных членов:
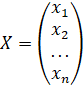
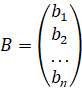
Тогда, используя правило умножения матриц,
систему можно записать в матричной форме: ![]() . Матрица A
имеет обратную, так как по условию
. Матрица A
имеет обратную, так как по условию ![]() . Умножая матичное уравнение
. Умножая матичное уравнение ![]() на обратную матрицу А-1
слева, получим
на обратную матрицу А-1
слева, получим
![]()
Следовательно, решение системы запишется в
виде ![]()
Пример
3.
Найти решение системы уравнений 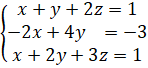
матричным способом.
Решение. Запишем
систему в матричном виде ![]() Здесь
Здесь
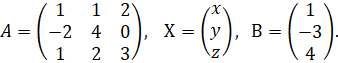
Вычислим определитель системы, используя его свойства:
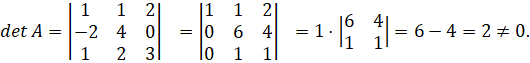
Обратная матрица имеет вид
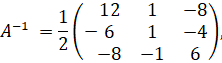
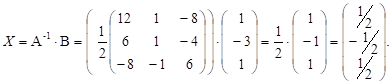 поэтому
поэтому
Пример
4.
Найти решение системы уравнений 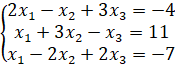
матричным способом.
Решение. Найдем обратную матрицу:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
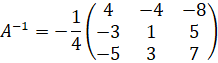
Тогда
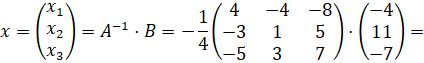
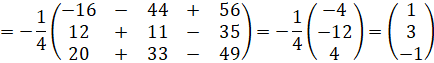
Следовательно, х1=1, х2=3, х3=-1.
3. Решение систем методом Гаусса
Рассмотрим систему линейных алгебраических уравнений общего вида
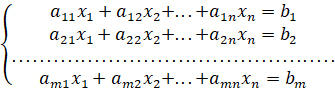
Введем две матрицы:
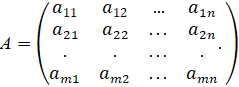
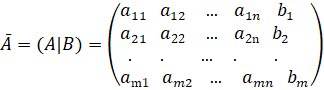
А
– матрица системы и матрица ![]() -
расширенная матрица, которая получается
-
расширенная матрица, которая получается![]() добавлением
к матрице
добавлением
к матрице![]() столбца свободных членов.
столбца свободных членов.
Метод Гаусса разделяется на 2 этапа. На 1 этапе пользуясь теоремой Кронекера-Капелли, необходимо выяснить совместность или несовместность системы уравнений. Если система совместна, то на 2 этапе нужно найти решения системы.
Теорема 1
(Кронекера-Капелли). Для того чтобы система (4) была совместной,
необходимо и достаточно, чтобы ранг матрицы ![]() был равен рангу расширенной
матрицы
был равен рангу расширенной
матрицы ![]()
При этом будем различать случаи:
1. система имеет единственное решение,
если ![]()
2. система имеет бесчисленное множество
решений, если ![]()
3. система не имеет решений, если ![]()
Здесь п- число неизвестных системы.
Замечание.
Для облегчения нахождения решения системы в случае ее совместности, удобнее
находить ранг матриц А и ![]() путем
приведения их к ступенчатому виду.
путем
приведения их к ступенчатому виду.
Пример 5. Найти все решения системы линейных уравнений
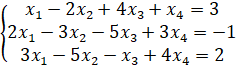
Решение. Будем рассматривать две матрицы
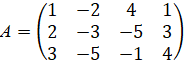 и
и 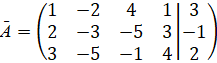
Найдем
ранги этих матриц, но так как матрица А полностью содержится в матрице ![]() , то можно привести матрицу
, то можно привести матрицу ![]() к
ступенчатому виду, сделать выводы о рангах матриц А
и
к
ступенчатому виду, сделать выводы о рангах матриц А
и ![]() ,
а
затем сделать выводы о совместности или несовместности системы уравнений.
,
а
затем сделать выводы о совместности или несовместности системы уравнений.
Найдем ранг матрицы ![]() .
.
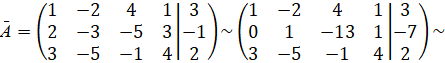
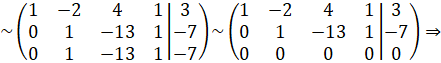
![]() система совместна.
система совместна.
![]() - число неизвестных. Следовательно, система
имеет бесчисленное множество решений.
- число неизвестных. Следовательно, система
имеет бесчисленное множество решений.
Чтобы найти эти решения, запишем последнюю матрицу в виде системы и найдем ее решения.
![]()
![]()
![]()
Пример 6. Найти все решения системы линейных уравнений
![]()
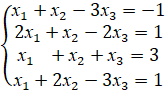
Решение. Будем рассматривать две матрицы
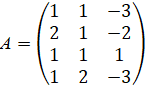 и
и 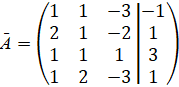
Приведем
матрицу ![]() к
ступенчатому виду.
к
ступенчатому виду.
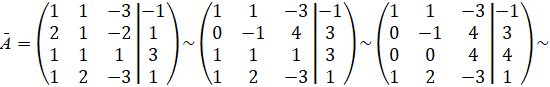
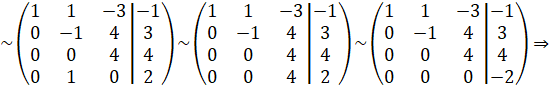
![]() система несовместна, то есть система
не имеет решений.
система несовместна, то есть система
не имеет решений.
Пример 7. Найти все решения системы линейных уравнений
![]()
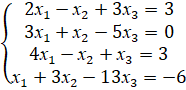
Решение. Будем рассматривать две матрицы
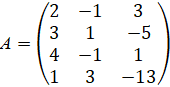 и
и 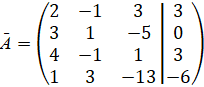
Приведем
матрицу ![]() к
ступенчатому виду.
к
ступенчатому виду.
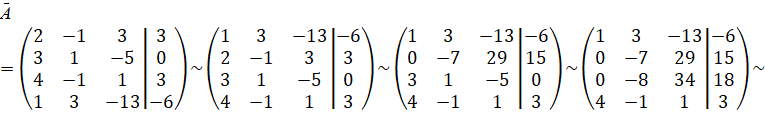
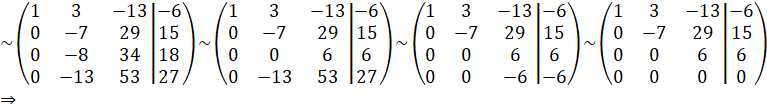
![]() система совместна.
система совместна. ![]() - число неизвестных. Следовательно, система
имеет
- число неизвестных. Следовательно, система
имеет
единственное решение.
Чтобы найти это решение, запишем последнюю матрицу в виде системы и найдем ее решения.