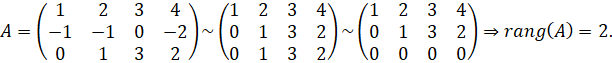Тема 1. Элементы линейной алгебры
Практическое занятие №2
Матрицы
Приведем примеры матриц:
; 
; 
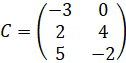и 
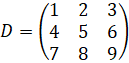
Размерности матриц соответственно равны: 2×3, 2×2, 3×2, 3×3.
Матрица, имеющая одинаковое число строк и столбцов, размерности п×п, называется квадратной матрицей порядка п. Матрица В – второго порядка, а матрица D – третьего порядка.
Треугольная матрица – это квадратная матрица, в которой элементы, расположенные под диагональю (или над диагональю), равны нулю. Например,
, 
, 
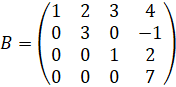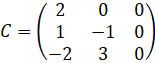- треугольные матрицы.
Квадратная матрица, все диагональные элементы которой равны 1, а остальные – нулю, называется единичной и обозначается Е.
Например,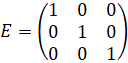 
- единичная матрица.
Действия над матрицами
1. Равенство матриц
Две матрицы называются равными, если матрицы имеют одинаковые размерности и элементы, стоящие на соответственных местах этих матриц, равны.
Пример 1.
Пусть даны две матрицы 
и 
. Если А=В, то a=2,
b=-4,
c=-1,
d=5.
2. Умножение матрицы на число
Чтобы умножить число 
на
матрицу 
или матрицу на
число , нужно умножить на все
элементы матрицы .
Пример 2. 
3. Сложение матриц
Суммой двух матриц 
~m×n
и
~m×n
одной размерности называется матрица 
~m×n
той же размерности (обозначается 
), элементы которой
определяются равенствами:
, 
.
Пример 3. Пусть
, 
.
Тогда 
.
Аналогично можно найти и разность матиц: 
4. Умножение матриц
В отличие от операций сложения и умножения на число операция умножения матрицы на матрицу определяется более сложным образом.
Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй:
, 
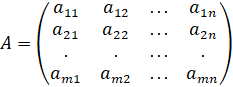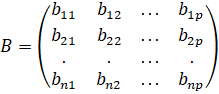
Положим 
. Матрица
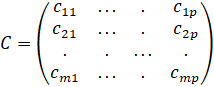
называется произведением A
на B и обозначается 
.
Замечание 2. Размерность
произведения матриц можно определить по правилу, которое в дальнейшем будет
называться правилом умножения размерностей:
.
Пример 4. Пусть
, 
.
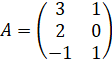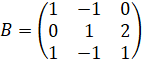Произведение матрицы
на матрицу
не определено, так как
число столбцов матрицы не равно числу строк
матрицы .
В то же время
произведение матрицы на матрицу определено,
причем 
имеет размерность 
. Действительно,
используя правило умножения размерностей, имеем
.
Согласно определению произведения матриц
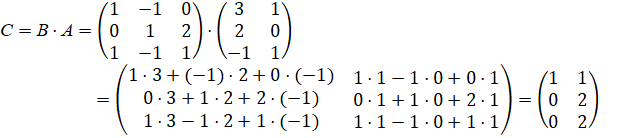
Произведение квадратных
матриц определено тогда и только тогда, когда эти матрицы имеют один и тот же
порядок n. При этом произведение так же будет квадратной
матрицей порядка n.
Пример 5 . Пусть
и 
. Имеем
, 
.
Таким образом, мы можем сделать важный вывод: при перемножении матриц нельзя менять порядок сомножителей.
5. Транспонирование матриц
Рассмотрим произвольную
матрицу А. Матрица АТ получающаяся из заменой
строк столбцами, называется транспонированной к .
Пример 6 .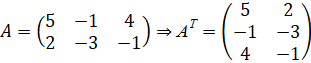 
6. Обратная матрица
Квадратная матрица 
называется обратной
к матрице, если имеет место
равенство: 
Не всякая квадратная матрица имеет обратную матрицу.
Матрица называется
невырожденной, если ее определитель отличен от нуля, и вырожденной в противном случае.
Для того чтобы матрица 
имела обратную матрицу,
необходимо и достаточно, чтобы она была невырожденной. При этом обратная
матрица находится по формуле:
, где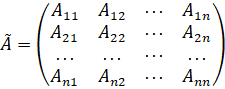 
.
Матрица 
называется присоединенной,
элементами этой матрицы являются алгебраические дополнения соответствующих
элементов матрицы А.
Пример 7.
Пусть
. Так как 
, матрица имеет
обратную. Найдем ее.
, 
, 
, 
;
, 
;
.
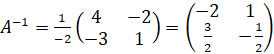Пример 8.
Пусть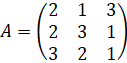
.
Так
как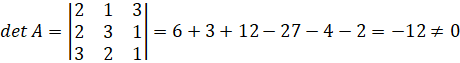 
матрица
имеет обратную.
Найдем обратную матрицу:
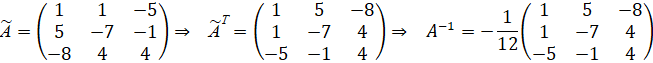
7. Ранг матрицы
Минором 
-го порядка матрицы
называется определитель,
образованный элементами, расположенными на пересечении каких-либо строк и каких-либо столбцов.
Пусть - матрица размера 
. Если матрица нулевая, то ее ранг
равен нулю. Если матрица ненулевая, то ее рангом
называется наибольший порядок 
минора, отличного от
нуля.
Пример 9. Вычислим
ранг матрицы , используя определение
ранга матрицы.
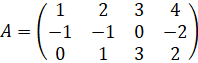
1) Рассмотрим миноры
первого порядка матрицы : среди них есть
ненулевые;
2) Существует минор второго порядка, отличный от нуля:
ранг не равен 1.
3) Рассмотрим миноры 3-го
порядка. Каждый из них лежит на пересечении всех трех строк матрицы и на пересечении
каких-либо трех из четырех столбцов матрицы . Поскольку
,
то в каждом из миноров
третья строка будет суммой первых двух. Поэтому все миноры третьего порядка
равны нулю, и тем самым 
.
Ступенчатой матрицей будем называть матрицу, удовлетворяющую следующим двум условиям:
1) все нулевые строки находятся ниже всех ненулевых;
2) у каждой ненулевой строки, кроме первой, число нулевых элементов, предшествующих первому ненулевому, больше, чем у предыдущей строки.
Например, ступенчатыми являются матрицы
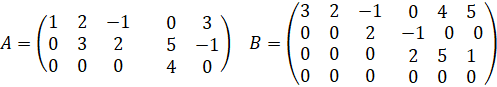
Частным случаем ступенчатой матрицы является треугольная матрица.
Ранг ступенчатой матрицы равен числу ее ненулевых строк.
В приведенных выше
примерах ступенчатых матриц: 
и 
Ранг матрицы удобно находить, приводя матрицу к ступенчатому виду. Такие преобразования возможно выполнить с помощью элементарных преобразований матриц.
Под элементарными преобразованиями матрицы понимаем:
1) перестановку строк;
2) умножение какой-либо строки на число, отличное от нуля;
3) сложение строк;
4) те же операции со столбцами.
Матрицы, полученные одна из другой элементарными преобразованиями, называются эквивалентными.
Эквивалентность матриц А и В обозначается символом ~: А~В.
Элементарные преобразования матрицы не меняют ее ранга.
Пример 10. Вычислим
ранг матрицы 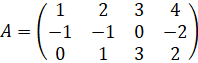, используя
элементарные преобразования матриц.
Решение. Чтобы привести матрицу к треугольному виду нужно выполнить преобразования, чтобы все элементы, расположенные ниже главной диагонали были равны нулю. Начинаем с первого столбца, все элементы кроме первого должны быть равны 0. Сначала прибавим ко второй строке первую строку. Получим две одинаковые строки. Чтобы получить 0 в третьей строке, нужно вычесть из третьей строки вторую строку. Получили ступенчатую матрицу. Ранг этой матрицы равен 2, так как в матрице 2 ненулевые строки.
