Дәріс 6. Синусоидалы тоқтың  сызықты электрлік тізбектері

6.1. RLC элементтерінің тізбектей жалғануы

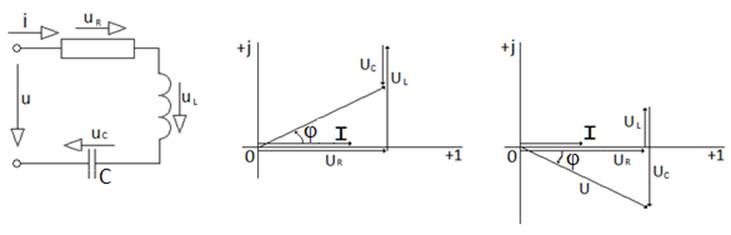
         Активті, индуктивті және сыйымдылық кедергілердің тізбектей жалғануы сур. 6.1а  көрсетілген.

                 а)                                          б)                                               в)

Сур. 6.1. Тізбектей қосылған RLC элементтер (а) және векторлық диаграммалар (б,в)

Тізбектен синусоидалы ток  i = I_{m *} sin ωt өтетін болса, лездік кернеуі Кирхгофтың 2-ші заңы бойынша активті кедергінің, индуктивтілік пен       сыйымдылықтың лездік кернеулерің қосындысынан тұрады:

u = u_R + u_L + u_C ,

немесе символикалық формада:

Ů_m = Ů_Rm + Ů_Lm + Ů_Cm = R İ_m + jX_L İ_m – jX_C İ_m ,

немесе әсерлік мәндері үшін:

Ů = [R+j(X_L -X_C)] _* İ = Z_* İ .              (6.1)

Комплекстік формамен жазылған Ом заңында (6.1)  Z = R+jX коплекс кедергі; Rактивті кедергі; X X_L -X_C = ωL -  реактивті кедергі.

        Активті кедергінің мәні R әрқашанда нөльден үлкен, ал реактивті кедергі Х болса, оның мәні оң және теріс болады, себебі ол индуктивті мен сыйымдылық кедергілердің айырымына байланысты. Активті кедергінің кернуінің векторы фаза бойынша токпен сәйкес келеді, индуктивтітіліктің кернеуі фаза бойынша токты 90° бұрышқа озып, ал сыйымдылықтың кернеуі фаза бойынша токты 90° бұрышқа қалып отырады.

       Берілген тізбекке векторлық диаграмма құру үшін екі жағдай болуы мүмкін: индуктивтітіліктегі кернеу сыйымдылықтағы кернеуден көп болған кезде (сур. 6.1б), яғни  U_L > U_C  (X_L >X_C), индуктивтітіліктегі кернеу сыйымдылықтағы кернеуден көп болған кезде (сур. 6.1в), яғни  U_L < U_C  (X_L <X_C).

        Векторлық диаграммадан алынған кернеулер үшбұрышынан берілген тізбек үшін толық кернеудің әсерлік мәні мынған тең:

U = 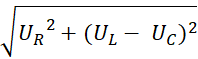              (6.2)

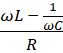немесе комплекстік формада  Ů = U , мұндағы  φ = arctg   – кернеу мен ток векторлары арасындағы бұрыш.

       Кернулер үшбұрышының әр жағын токқа бөлсе, кедергілер үшбұрышын алуға болады (сур. 6.2а). Ал кедергілер үшбұрышын әр жағын ток квадратыга көбейткенде, қуатар үшбұрышын алуға болады (сур. 6.2б).

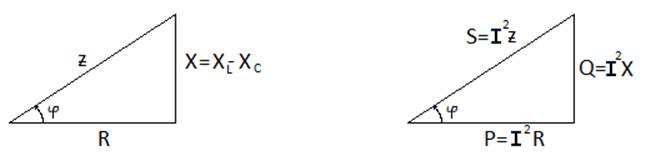
                     а)                                                                 б)

        Сур. 6.2. Кедергілер (а) және қуаттар (б) үшбұрыштары

Қуат үшбұрышында  S [ВА] – толық қуат, P [Вт] – активті қуат,  Q [ВАр] – реактивті қуат.

Қуат үшбұрышы бойынша

S = zI² = UI,  P = RI² = UI *cos φ, Q = XI² = (X_L -X_C)I² = UI *sin φ    (6.3)

Толық қуаттың компекстік шама тең:

Ṡ = P+jQ = Ů I^*                              (6.4)

мұнда  I^* – токтын түйіндескен векторы.

6.2. RLC элементтерінің паралель жалғануы

          Параллель тізбекке түсірілген кернеудің лездік мәні  u =  (сур. 6.3а).

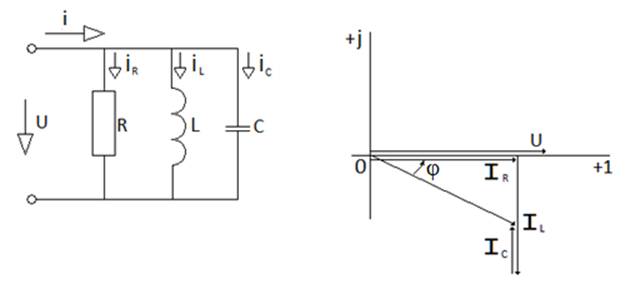
                          а)                                                           б)

Сур. 6.3. Параллель қосылған RLC элементтер (а) және векторлық диаграмма (б)

Кирхгофтың бірінші заңына сәйкес тармақтардағы токтардың лездік мәндері  i = i_R + i_L + i_C.

Ом заңын коплекс форманы қолданып, әр тармаққа мына формуларды аламыз:

İ_R = ,  İ_L = ,  İ_C = j.

Комплекс токтардың өрнектерін Кирхгофтың бірінші заңына қойып, мынаны аламыз:

İ =  +  + j= ( - j  + j= [ - j –

                 = [g –j(b_L – b_C)]  = (g –jb)  = Y*                  (6.5)

мұндағы  g – активті өткізгіштік,  b – активті өткізгіштік,  Y – комплекс өткізгіштік. Комплекс өткізгіштік комплекс кедергіге кері шама ретінде анықталады:

Y =  =  =  =  -  = g –jb = y,

мұндағы  g =  – активті өткізгіштік,  b =  – реактивті өткізгіштік,

y = – толық өткізгіштік,   = - arctg – ток пен кернеудің арасындағы фазаның ығысуы.

Комплекс токтың өрнегіне (6.5) сәйкес токтардың векторлық диаграмма  6.3б суретінде көрсетілген.

6.3. Резонанс құбылыстары

       Индуктивтілік пен сыйымдылығы бар айнымалы ток тізбектерінде резонанс құбылыстары пайда болады. Резонанстық режим деп RLC электр тізбегінің реактивті кедергісін болмаса реактивті өткізгіштігін нөльге теңестіретін режимін айтады. Мұндай режимде ток пен кернеудің фазалары бір-біріне тең, ал тізбектің эквиваленттік комплекс кедергесі активті кедергісімен сипатталады.

6.3.1. Кернеулер резонансы

Кернеулер резонансы тек қана RLC элементтердің тізбектеліп байланысқан схемаларында ғана орын алады (сур. 6.1а). Бұл жағдай тек қана реактивті кедергі нөльге тің болғанда ғана орындалады, сол себепті

X = ωL -  = 0, немесе ωL = .           (6.6)

(6.6) арқылы резонансты жасау үшін, токтын жиілікті өзгертіп, резонанстық жиілікке ω₀  жеткізу керек, индуктивтілік пен сыйымдылықты тұрақты үстап:

ω₀ =

        Резонанс кезінде X_L = X_C немесе   – индуктивтілік пен сыйымдылықтының кернеулері бір-біріне тең болған кейін, векторлық диаграмма бойынша (сур. 6.4а) резистордағы кернеу кірістік кернеуге тең

U = U_R, тізбек таза активті (φ =0).

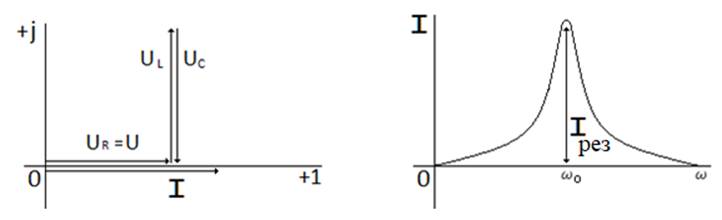
                                а)                                                                б)

Сур. 6.4. Векторлық диаграмма кернеулер резонанс кезінде (а)

және токтың жиілікті сипаттамасы (б)

        Ом заңы бойынша токтын күші

I =  = 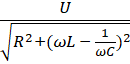.            (6.7)

Токтын жиілікті сипаттамасы  I = f (ω) сур. 2.10б көрсетілген.  ω = 0 және

ω = ∞ ток жоқ (І = 0), резонанс кезінде ω = ω₀ токтын күші максимал:  I_рез = .

6.3.2. Токтар резонансы

Токтар резонансы RLC элементтеінен құрылған параллель тізбекте туындайды (сур. 6.3а). Токтар резонансы деп реактивті өткізгіштігі нөльге тең болған кездегі (b = b_L – b_C = 0) параллель тізбектің режимін атайды. Индуктивті және сыйымдылық өткізгіштіктердің бір-біріне тең  b_L = b_C болғандықтан   . Осы шарттан токтың резонастық жиілігі  ω₀ =

кернеу резонансының жиілігіне тең.

        Резонанс кезінде Ом заңымен табылатын реактивті токтар (I_L = U*b_L ,

 I_C = U*b_C) бір-біріне тең болған кейін I_L = I_C, векторлық диаграмма бойынша (сур. 6.5а) резистордағы ток кірістік токқа тең  І = І_R = U*g , тізбек таза активті (φ =0).

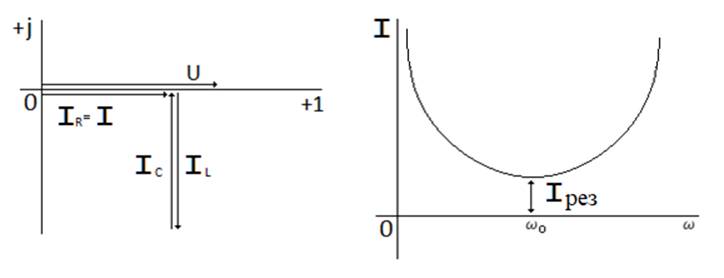
                              а)                                                         б)

Сур. 6.5. Векторлық диаграмма токтар резонанс кезінде (а)

және токтың жиілікті сипаттамасы (б)

       Ом заңы бойынша токтын күші

I = y _* U = 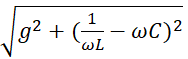_* U.          (2.50)

Токтын жиілікті сипаттамасы  I = f (ω) сур. 6.5б  көрсетілген. ω = 0 және

ω = ∞ ток шексіз болады  (І = ∞), резонанс кезінде  ω = ω₀  токтын күші минимал:  I_рез = g _* U.