Дәріс 5. Айнымалы ток тізбегіндегі пассивтік элементтері

 5.1.1. Резистордағы (активтік кедергідегі) синусоидалы ток

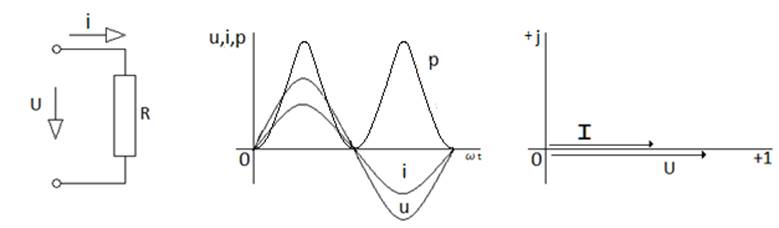
       Активтік кедергіні (сур.5.1а) айнымалы кернеуге u = U_{m *} sin ωt қоссақ,

               а)                                          б)                                               в)

Сур. 5.1. Резистор (а); кернеу, ток, қуат графигі (б); векторлық диаграмма (в)

 резистор арқылы синусоидалы ток жүреді (сур.5.1б) Ом заңы бойынша:

i =  * sin ωt = I_{m *} sin ωt,  I_m =  .                           (5.1)

Немесе Ом заңы комплекстік әдісте Ů = R* İ.                              (5.2)

Активтік кедергінің кернеудің және токтың бастапқы фазалар бірдей болады. Бірдей жиіліктері бар екі синусоиданың бастапқы фазаларының айырымын фазалық ығысу φ деп атайды. Берілген жағдайдағы кернеумен токтың арасындағы фазалық ығысу нөлге тең:  φ = ψ_u –ψ_i = 0 (сур. 5.1в кернеумен токтың векторлары сәйкес бағытталған).

        Қарастырлып отырған активтік кедергіден тұратын тізбектің лездік қуаты p [Вт] кернеумен токтың лездік мәндерінің көбейтіндісіне тең:

p= u*i = _* I_{m *} sin² ωt = _* I_{m *} (1- cos2ωt) = I _* (1- cos2ωt).   (5.3)

        Лездік қуаттың графигі сур. 5.4б  көрсетілген. Бір период ішіндегі активтік кедергінің лездік қуаттың орташа мәні лездік қуаттың тұрақты кұраушысына тең активтік қуат  Р [Вт] деп аталады да, келесі формула бойынша анықталады:

P = I = I² _* R.                (5.4)

Айнымалы ток тізбегіндегі активті кедергі үшін жазылатын қуаттын формуласы (5.4) тұрақты ток тізбегі үшін жазылатын қуаттын формуласына ұқсас.

5.1.2. Индуктивті кедергідегі синусоидалы ток

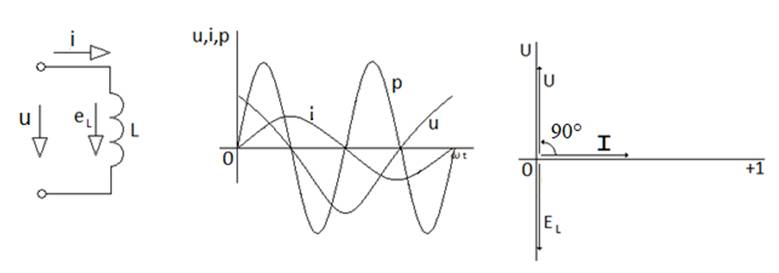
       Индуктивті катушканың айнымалы тогы (сур. 2.5а) айнымалы магнит өрісін тудырады. Айнымалы магнит өрісі, электромагниттік заңы бойынша, катушкасысының орамдарында ЭҚК индукциялайды. Өздік индукцияның ЭҚК-ін бағыты, Ленц ереже бойнша, туындатып отырған токтың өзгеруіне

          а)                                                   б)                                               в)

Сур. 5.5. Индуктивтілік (а); кернеу, ток, қуат графигі (б); векторлық диаграмма (в)

қарсы бағытталған. Осылайша, индуктивтік катушкасы бар тізбектің бойымен  айнымалы токтың өтуіне өздік индукцияның ЭҚК қарсы әрекет жасайды. Бұл құбылыс индуктивтік катушкасының айнымалы токқа көрсететін кедергісін білдіреді.

       Индуктивтік катушкасының кедергісі реактивтік индуктивтік кедергі X_L[Ом]  деп аталады. Катушканың индуктивтілігі  L[Гн] белгілі болса, реактивтік кедергісі келесі формуламен анықталады:

X_L = ωL = 2πf L, (5.5)

ал индуктитік өткізгіштікті  b_L [См] мындай формуламен

b_L =  = .                            (5.6)

       Идеалды катушкадан (шығындары жоқ) синусоидалы ток i = I_{m *} sin ωt өтетін кезде лездік кернеу электромагниттік индукция заңы бойынша табылады:

u = e = L  = L_* I_{m *} ω_* cos ωt = X_L I_m sin(ωt+ (5.7)

мүнда = = X_L I_m  – кернеумен ЭҚК-ің амплитудалары. Осы өрнектін мүшелерін    бөлсек, онда Ом заңы ток пен кернеудің әсертеуші мәндері үшін келесідей жазылады: U = E = X_L I.  (5.7) формуласынан көрініп тұрғандай индуктивті кернеу токтан фаза бойынша  -ге озады (сур. 5.5б). Олай болса, индуктивті катушкаға арналған Ом заңы символикалық әдісімен былай жазылады:

Ů = Ė = jX_L İ.          (5.8)

(5.8) бойынша 5.5в-суретте векторлық диаграмма салынды. Мұнда кернеу векторы Ů ток векторынан İ 90°-қа алға қарай бұрылған, фазалық ығысуы  -ге тең болады, яғни  φ = ψ_u –ψ_i = .

        Лездік қуатты бұрынғыдай анықтайық:

p= u_* i = _* I_m  sin ωt = 2ωt = I _* sin2ωt.   (5.9)

Бір период ішінде индуктивті кедергідегі қуаттын орташа мәні нөльге тең. Энергия көзі мен индуктивті кедергі арасында ешқандай жұмыс тудырмайтын электр энергтясының ұзіліссіз циркуляция (айналымы) пайда болады. Идеалды индуктивтітіліктің активті қуаты нольге тең болса, оның реактивті қуаты  Q_L [ВАр] мынаған тең:

Q_L = U_* I = I² X_L.                    (5.10)

5.1.3. Сыйымдылықтағы синусоидалы ток

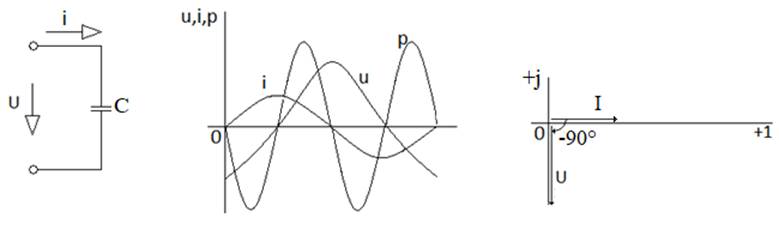
        Электр конденсатордың екі пластинасына әраттас зарядталса, бұлардын арасында электр өріс туады. Электр орісінің энергиясы жинақталатын конденсатордың қасиетіне жақын келетін электр тізбегінің идеал элементін сыйымдылық деп атайды  (сур. 5.6а).

          а)                                           б)                                               в)

Сур. 5.6. Индуктивтілік (а); кернеу, ток, қуат графигі (б); векторлық диаграмма (в)

        Сыйымдылық  С [Ф] элементтегі зарядты кернеуге қатынасының сандық шамасын көрсетеді:

C = .                                      (5.11)

Ток электр зарядының уақыт бойынша туындысына тең:

i =  = C                            (5.12)

Егер сыйымдылықтан синусоидалы ток i = I_{m *} sin ωt өтетін болса, онда сыйымдылықтың кернеу тең:

u =  ∫idt =  ∫I_{m *} sin ωt dt = cos ωt =  _* .      (5.13)

(5.13) формуласынан көрініп тұрғандай сыйымдылықтың кернеуі синусоидалық заң бойынша өзгереді және фаза бойынша токтан  -ге қалып отрады (сур. 5.6б). (5.13) сонғы өрнектегі бірінші мүшесін реактивтік сыйымдылық кедергі  X_С[Ом]  деп аталады. Онын мәні

X_С =  = ,            (5.14)

ал сыйымдылық өткізгіштікті  b_С [См] мындай формуламен табылады:

b_С =  = .                  (5.15)

Олай болса, сыйымдылыққа арналған Ом заңы символикалық әдісімен былай жазылады:

  Ů = j X_С İ.            (5.16)

(5.16) бойынша 5.6в- суретте  векторлық диаграмма салынды. Мұнда кернеу векторы Ů ток векторынан İ 90°-қа артқа қарай бұрылған, фазалық ығысуы  -ге тең болады, яғни  φ = ψ_u –ψ_i = .

        Лездік қуатты бұрынғыдай анықтайық:

p= u_*i = _* I_m  sin ωt = 2ωt = I _* sin2ωt.   (5.17)

Конденсатордың лездік қуаты ток пен кернеудің өзгеру жиілігімен салыстырғанда екі еселенген жиілікпен өзгереді. Демек, бір период ішінде сыйымдылықтың орташа қуаты нөльге тең. Реактивті қуаты Q_С [ВАр] мына формуламен анықталады:

Q_С = U_* I = I² X_С.                    (5.18)

5.4. Айнымалы токтың электр тізбегінің табиғаты

        Жоғарыда айнымалы ток электр тізбектерінің идеалды элементтерінің сипаттамаларын қарастырдық. Нақты электр жабдығы идеалдыдан белгілі бір дәрежеде ерекшеленетін элементтерден тұрады, сондықтан айнымалы ток тізбектері тәжірибеде бір-бірімен сол немесе басқа жолмен қосылған элементтердің жиынтығы болып табылады.  Мысалы, электр машиналары мен трансформаторлардың орамдары алюминий немесе мыс сымдардан жасалған, олар индуктивті кедергімен бірге активті кедергіге ие. Белгілі бір элементтердің басым болуы синусоидалы токтың электр тізбегінің сипатын анықтайды.

5.4.1. Тізбектің активті-индуктивті сипаты

Айнымалы ток тізбектерінің ішінде ең көп таралғаны индуктивті катушкалар мен резистордың тізбектей қосылуы болып табылады (5.7-сурет).

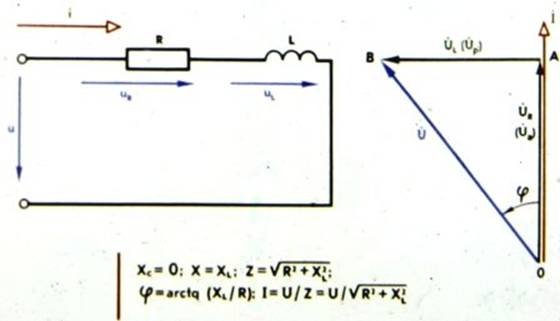
5.7-сурет. Активті кедергі мен индуктивтіліктің тізбектей қосылуы

         Бұл жағдайда кіріс кернеуі резистор мен катушка кернеулерінің қосындысына тең:

                                Ů = Ů_R + Ů_L = R İ + jX_L İ.                  (5.19)

 (5.19) үшін векторлық диаграмма 5.7-суретте көрсетілген (ағымдық вектор тігінен бағытталған). Кіріс кернеуінің векторы  Ů  ток  İ  векторын

φ = arctg (X_L / R)  бұрышымен жүргізеді.

          (5.19) ның сол және оң жақ бөліктерін комплексті  İ  токына бөлсек, мынаны аламыз:

Z = R + jX_L = z e ^jφ,                  (5.20)

мұндағы  Z – тізбектің толық комплекстік кедергісі;

R – тізбектің активті кедергісі;

X_L – катушканың индуктивті кедергісі;

z – тізбектің толық кедергісі;

φ – кіріс кернеуі мен ток арасындағы фазалық ығысу.

         Кіріс кернеуінің векторы ток векторын φ > 0 бұрышпен жүргізетін айнымалы токтың электр тізбегі активті-индуктивті сипатқа ие.

5.4.2. Тізбектің активті-сыйымдылық сипаты

         Активті кедергі мен сыйымдылықты тізбектей қосқанда (5.8-сурет) кіріс кернеуі резистор мен конденсатордың кернеулерінің қосындысына тең болады:

Ů = Ů_R + Ů_С = R İ - jX_С İ.                  (5.21)

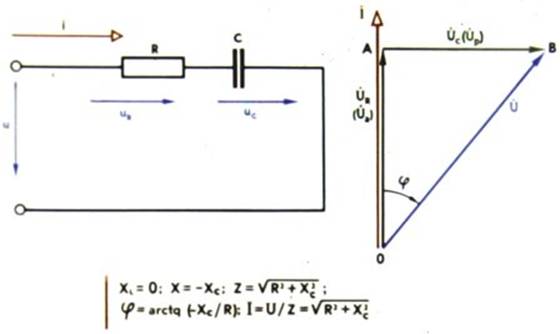
5.8-сурет. Активті кедергі мен сыйымдылықты тізбектей қосу

(5.21) үшін векторлық диаграмма 5.8-суретте көрсетілген (ағымдық вектор тігінен бағытталған). Онда кіріс кернеу векторы  Ů  ток  İ  векторынан

φ = arctg (X_С / R) бұрышымен артта қалады.

          (5.19) ның сол және оң жақ бөліктерін комплексті  İ  токына бөлсек, мынаны аламыз:

Z = R + jX_L = z e ^jφ,                  (5.20)

мұндағы  Z – тізбектің толық комплекстік кедергісі;

R – тізбектің активті кедергісі;

X_С – тізбектің сыйымдылық реактивтілігі кедергісі;

z – тізбектің толық кедергісі;

φ – кіріс кернеуі мен ток арасындағы фазалық ығысу.

         Ток векторы кіріс кернеуінің векторын φ < 0 бұрышпен жүргізетін айнымалы ток электр тізбегі активті-сыйымдылық сипатына ие.

5.4.3. Реактивті ток өтемі

         Электр энергетикалық жүйелерде жүктеме активті-индуктивті сипатта болады. Жүктеменің индуктивті құрамдас бөлігі неғұрлым көп болса, соғұрлым фазалық коэффициент cos φ төмен болады - энергетикалық жүйенің негізгі экономикалық көрсеткіші.  φ  бұрышын азайту және кіріс тоғының реактивті компонентін азайту үшін резистор мен катушканың тізбекті тізбегіне параллель конденсаторлар батареясы қосылады (5.9-сурет).

         Кирхгофтың бірінші заңы бойынша  İ  кіріс тогы актив-индуктивті тармақтың ток  İ₁  және конденсатор  İ₂  сыйымдылық тоғының қосындысынан тұрады:

İ = İ₁ + İ₂.                  (5.23)

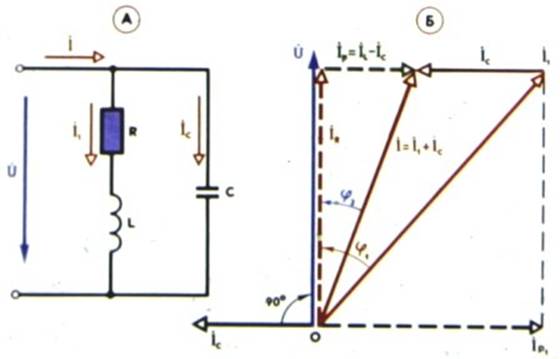
5.9-сурет. Конденсатор мен активті кедергісі және индуктивтілігі бар тармақтың параллель қосылуы

         Кирхгофтың бірінші заңы бойынша  İ  кіріс тогы актив-индуктивті тармақтың ток  İ₁  және конденсатор  İ₂  сыйымдылық тоғының қосындысынан тұрады:

İ = İ₁ + İ₂.                  (5.23)

        Тізбектің векторлық диаграммасынан (5.9-сурет) көрініп тұрғандай, кіріс кернеуі мен ток арасындағы фазалық ығысу  φ₁-ден  φ₂-ге дейін төмендейді. Сәйкесінше, фазалық коэффициент  cos φ₁-ден  cos φ₂-ге дейін артады. Осылайша, токтың реактивті құрамдас бөлігі мен энергетикалық жүйенің реактивті қуатының компенсациясы орын алады.

5.4. Характер электрической цепи переменного тока

        Выше рассмотрены характеристики идеальных элементов электрических цепей переменного тока. Реальное электрооборудование состоит из элементов в той или степени отличющихся от идеальных, поэтому цепи переменного тока  на практике представляют собой совокупность элементов, соединенных между собой тем или иным способом. Так, например, обмотки электрических машин и трансформаторов выполняются из алюминиевых или медных проводов, которые наряду с индуктивным обладают активным сопротивлением. Преобладание тех или иных элементов определяет характер электрической цепи синусоидального тока.

5.4.1. Активно-индуктивный характер цепи

        Среди цепей переменного тока наиболее часто встречается последовательное соединение индуктивной катушки и резистора (рис. 5.7).

Рис. 5.7. Последовательное соединение активного сопротивления и индуктивности

        В этом случае входное напряжение равно сумме напряжений резистора и катушки:

Ů = Ů_R + Ů_L = R İ + jX_L İ.                  (5.19)

Векторная диаграмма  по (5.19) показана на рис. 5.7 (вектор тока направлен вертикально). Вектор входного напряжения  Ů  опережает ветор тока  İ  на угол  φ = arctg (X_L / R)

        Разделив левую и правую части (5.19) на комплексный ток  İ,  получим:

Z = R + jX_L = z e ^jφ,                  (5.20),

где  Z – полное комплексное сопротивление цепи;

R – активное сопротивление цепи;

X_L – индуктивное сопротивление катушки;

z – полное сопротивление цепи;

φ – сдвиг по фазе между входными напряжением и током.

        Электрическая цепь переменного тока, у которой вектор входного напряжения опережает вектор тока на угол  φ = 0, имеет активно-индуктивный характер.

5.4.2. Активно-емкостный характер цепи

        При последовательном соединение резистора и конденсатора  (рис. 5.8)

случае входное напряжение равно сумме напряжений резистора и катушки:

Ů = Ů_R + Ů_L = R İ + jX_L İ.                  (5.21)

Рис. 5.8. Последовательное соединение активного сопротивления и емкости

Векторная диаграмма  по (5.21) показана на рис. 5.8 (вектор тока направлен вертикально). Вектор входного напряжения  Ů  отстает от ветора тока  İ  на угол  φ = arctg (X_С / R)

        Разделив левую и правую части (5.20) на комплексный ток  İ,  получим:

Z = R - jX_с = z e ^jφ,                  (5.22),

где  Z – полное комплексное сопротивление цепи;

R – активное сопротивление цепи;

X_С – индуктивное сопротивление катушки;

z – полное сопротивление цепи;

φ – сдвиг по фазе между входными напряжением и током.

        Электрическая цепь переменного тока, у которой вектор тока опережает вектор входного напряжения на угол  φ = 0, имеет активно-емкостный характер.

5.4.3. Компенсация реактивного тока

         В электроэнергетических системах нагрузка носит активно-индуктивный характер. Чем больше индуктивная составляющая нагрузки, тем ниже коэффициент фазы  cos φ – главный экономический показатель энергосистемы. Для уменьшения угла  φ  и снижения реактивной составляющей входного тока к последовательной цепи резистора и катушки параллельно подключают батарею из конденсаторов (рис. 5.9).

Рис. 5.9. Параллельное соединение емкости и ветви с активным сопротивлением и индуктивностью

        По первому закону Кирхгофа входной ток  İ состоит из суммы тока  İ₁ активно-индуктивной ветви и емкостного тока конденсатора  İ₂:

İ = İ₁ + İ₂.                  (5.23)

Как видно из векторной диаграммы цепи (рис. 5.9), сдвиг по фазе между входными напряжением и током уменьшается от  φ₁ до φ₂. Соответственно коэффициент фазы повысится от значкния  cos φ₁ до  cos φ₂. Таким образом, происходит компенсация реактивной составляющей  тока и реактивной мощности энергосистемы.