Дәріс 4. Синусоидалы тоқ және  символдық әдіс

4.1. Бір фазалы синусоидалық ток және оның шамалар

      Өзінің бағыты және шамасы периодты түрде өзгеріп отыратын токты (кернеуді) айнымалы деп атайды. Синусоидалық ток уақытқа байланасты синусоидалық заңымен өзгереді (сур. 4.1):

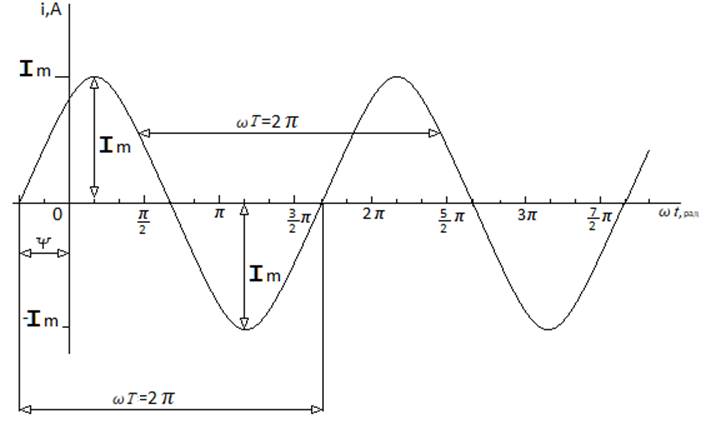
                                Сур. 4.1. Синусоидалық токтын графикі

і(t) = I_{m *} sin(ωt +ψ),                   (4.1)

мұнда і [A] – токтын лездік мәні (кез келген уақыт моменті үшін токтын күші);

І_m [A] – амплитуда (функцианың максимал шамасы);

ω [] – бұрыштық жиілік (жылдамдық);

t [c] – уақыт;

Ψ [рад] – функцияның бастапқы фаза;

(ωt +ψ) [рад] – фаза (синустын аргументы). Фаза t-уақыт кезеңіндегі тербелістің күйын (сан мәнін) сипаттайды.

Толық бір тербеліс жасауға кететін уақытты период Т[c] деп атайды. Периодқа кері шаманы жиілік f [Гц] деп аталады:  f = 1/T  (бір секундтағы тербелістер саны). Олай болса  ω = 2π*f = 1/T.                (4.2)

        Жоғары математикада f (t) периодтық функцияның Т- периодындағы орташа мәні мындай өрнекпен анықталатыны белгілі:

F_орт =                      (4.3)

Синусоидалық функция жағдайнда период ішіндегі оның мәні нөлге тең. Сондықтан айнымалы токтын орташа мәні І_орт орташа жартыпериодтың (Т/2) мәні алынады (ψ = 0):

І_орт = = . (4.4)

Осыған ұқсас E_орт = U_орт =        (4.5)

      Жалпы қолданыстағы барлық құралдар әсерлік мәнін көрсетеді (амперметрлер, вольтметрлер және т. б.). Математикалық жолмен әсерлік мән I келесідей анықталады:

I =  =  =

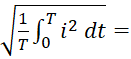
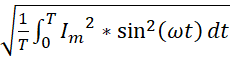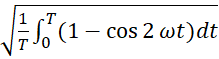.                                        (4.6)

Осыған ұқсас  E =     U =          (4.7)

Синусоидалы шамаларың әсерлік мәндері олардың амплитудалық мәндерінен  есе аз. Синусоидалық ток әрекеттік мәні кедергі арқылы жүрген кезде бір период ішінде қанша жылу бөлсе, сонша уақытта сондай жылу бөліп шығаратын тұрақты токтын мәніне тең.

4.2. Cимволдық әдіс

4.2.1. Cинусоидалық токтарды комплестік

жазықтықта кескіндеу

       Синусоидалы ток тізбегін есептеген кезде ток пен кернеудің лездік мәндерін пайдаланудың қажеттіліғі туындайды. Яғни, барлық математикалық операцияларды тригонометриялық функциялар арқылы шешуге тура келеді. Есептің шешімін жеңілдету үшін, математика курсынан белгілі , кез келген синусоидалы функцияны векторлық шама арқылы өрнектеуге болатындығын пайдаланады.

        Математика курсынан белгілі Эйлер өрнегі бойынша

 = cos α +jsin α, (4.8)

Мұнда  j =  – жорамалдық бірлік, комплекстік жазықтағы оған көбейту вектордын рад немесе 90° сағат тіліне қарсы бұрылу болады. Комплекстік жазықтағы (сур. 4.2а) комплекстік саны векторды бейнелейді, ол бірге тең және заттық мәндер өсімен (+1)  α-бұрыш жасайды. α-бұрыш +1 осінен

сағат тілі бағытына қарсы бағытқа саналады. Функіиянын модулі  || =  =1. Мұндағы -функциясы +1 өсіне проекциясы cos α-ға, ал +j жорамал мәндер өсіне проекциясы sin α-ға тең болады.

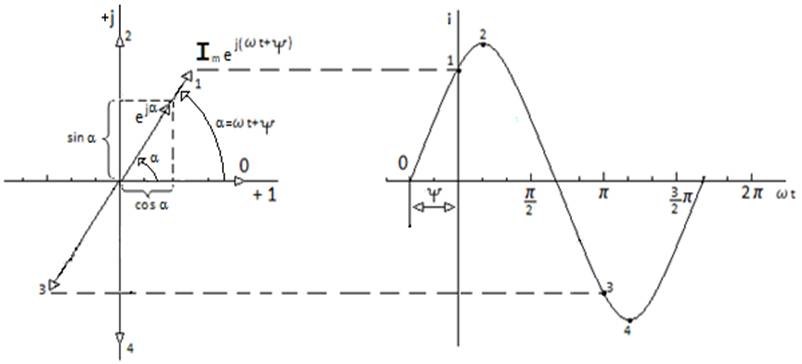
                 а)                                                                        б)

Сур. 4.2. Бірлік және лездік токтын векторлар (а), вектор проекциялаған

                токтын графикі (б)

         Егер -функциясының орнына  -ны алсақ, онда

= cos α + j*sin α                                (4.9)

(4.8) өрнегіндегі α-бұрышы кез-келген бола алады. Сондықтан біз  α = ωt +ψ деп, яғни α-бұрышы уақытқа байланасты тура пропорционал өзгереді деп алайық. Сонда

 = cos(ωt +ψ) + jsin(ωt +ψ). (4.10)

Мұнда  cos(ωt +ψ) қосылғышы  -дің нақты бөлігін (Re) құрайды, сондықтан 

cos(ωt +ψ)= Re ,                               (4.11)

ал  sin(ωt +ψ) функциясы  өрнегінің жорамал болігі (Im) болып табылады, демек

sin(ωt +ψ) = Im . (4.12)

Сонымен синусоидамен өзгеретін (4.1) және і-тогын  Im  түрінде, немесе дәл осы сияқты, бірақ   айналу векторының  +j осіне проекциясы түрінде көрсетуге болады (сур. 4.2б).

        Комплекстік жазықтықтарда уақытқа байланасты синусоидалық түрде өзгеретін вектордын (ωt=0 болатын уақыт кезеңіндегі) шамасы қабылданған. Сонда вектор мынадай  болады:

 =  = İ_m         (4.13)

Мұндағы    – і-токтын комплекстік амплитуда, модулі токтын амплитудасына  –ге тең комплекстік шама; ψ – бастапқы фазаға тең,  жазықтықтың  +1 өсіне  -векторының жасайтын бұрышы.  Токтың (ЭҚК-нің, кернуінің) үстіне қойылған нүкте бұл  шаманың уақытка байланасты синусоида заңымен өзгеретінін көрсетеді.

       Токтың әсерлік мәнінің комплексі немесе комплекстік ток İ деп комплекстік амплитуданы  –ге бөлгендегі бөліндіні атайды:

İ =  I.           (4.14)

Сол сияқты комплекстік ЭҚК және кернеу

Ė =  =  =E,  Ů =  =  =U       (4.15)

       Сонымен синусоидамен өзгеретін токтарды, кернеулерді, ЭҚК-ді (немесе комплекстік амплитудаларды) екі түрімен жазуға болады:

       Айнымалы ток тізбегін есептеу  үшін комплексті сандарды пайдаланатын әдіс комплексті немесе символдық әдіс деп аталады. Әдіс бойынша комплексті саны екі түрімен жазуға болады:

көрсеткіштік формасы    İ  I,                                                          (4.16)

алгебралық формасы    İ = Re İ + j Im İ =  + j ,                              (4.17)

мұнда І – саның модулі, ψ - бастапқы фаза, 

 =  І*sinψ – активті құраушы,  = І*cosψ – реактивті құраушы,    (4.18)

І = 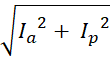,  ψ = arctg  .                                                                  (4.19)

4.2.2. Cимволдық әдісінің ережелері

         Жиіліктері бірдей екі токты і₁ = I_{1m *} sin(ωt +ψ₁) және і₂ = I_{2m *} sin(ωt +ψ₂) қосу керек болсын. Сонда олардын қосындылары сондай жиілікті токты береді:

i = і₁+ і₂ = I_{m *} sin(ωt +ψ).                   (4.20)

Демек, i-токтын амплитудасын I_m , бастапқты ψ анықтау қажет.

         Осыған сәйкес комплекстік жазықтықта (сур. 4.3) екі тогын İ_1m =  және İ_2m =  векторлары түрінде бейнелейміз.

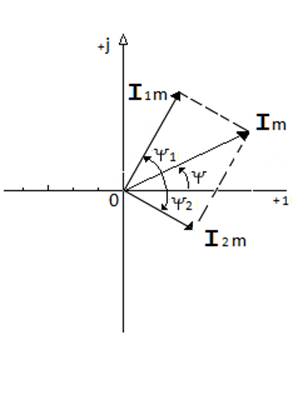
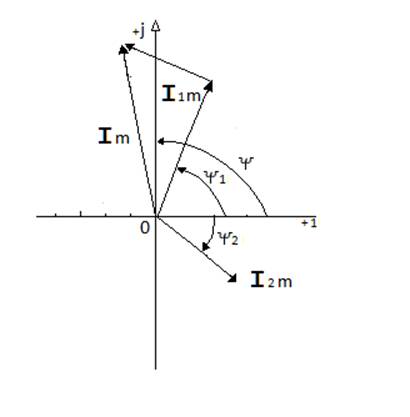
                            а)                                                          б)      

Сур.4.3. Комплекс сандарды қосу (а) және айырту (б) комплекстік жазықтықта

İ_1m және İ_2m векторларының геометриялық қосындылары  İ_m = қосынды, токтын коплекстік амлитудасын береді. Токтың  -амплитудасы қосынды вектордың ұзындығы, ал бастапқы  ψ-фазасы осы вектор мен  +1 осінің арасындағы бұрыш ретінде анықталады.

Векторлық диаграмма (сур. 4.3) деп біз уақыт бойынша бірдей жиілікпен синусоида заңымен өзгеретін, фазаларына байланысты бір-бірмен салыстырғанда, дұрыс бағытталулары сақтала отырып салынған, комплекстік жазықтықтағы векторлардың жиынтығын айтамыз.

        Векторлық диаграмма (сур. 4.3а) мындай ережеге келтіреді.

Комплекс сандары қосу кезінде олардың нақты және жорамал бөліктері жеке жеке қосылады:

( + j)++ j+ j

(2.21), мұнда    қосынды İ_m- комлекстын нақты және  жорамал бөліктері.

         Екі токтың (кернудің, ЭҚК-нің) айырымын анықтау үшін, комплекстік жазықтықта қосу операцияның орнына тиісті векторлардың айырымын аныұтау операциясын жүргізу керек (сур. 4.3б). Комплекстарды алгебралық формамен усынатқанда.

Комплекс сандары айырту кезінде олардың нақты және жорамал бөліктері жеке жеке айырады:

( + j)-+ j+ j

(2.22), мұнда    қосынды İ_m- комлекстын нақты және   жорамал бөліктері.

       Көрсеткіштік формада өрнектелген комплекс сандарды İ₁  және İ₂ = көбейту ыңғайлы:

İ İ_1* İ₂ = _*  = _*  = I,          (4.23)

мұнда I = _*  – көбейтіндінің модулі, ψ = ψ₁ +ψ₂ – көбейтіндінің аргументі.

Комплекс сандары көбейту кезінде көбейтіндінің модулі көбейткіштердің модульдерінің көбейтіндісіне, ал көбейтіндінің аргументі көбейткіштердің аргументтерінің қосындысына тең.

         Көрсеткіштік формада өрнектелген комплекс сандарды бөлу ыңғайлы:

İ İ₁/ İ₂ = /  = /  = I,          (4.24)

мұнда I = /  – көбейтіндінің модулі, ψ = ψ₁ -ψ₂ – көбейтіндінің аргументі.

Комплекс сандары бөлу кезінде қалдығынің модулі сандардың модульдерінің бөлуіне, ал аргументі сандардың аргументтерінің айыруына тең.