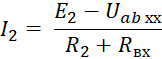Дәріс 3. Электр тізбектерді есептеу әдістері

3.1. Кирхгоф заңдары қолданылуы

Кирхгофтың заңдары схеманың тармақтарындағы (тармақтағы элементтерінің параметрлері белгілі кезінде) токтарды табу үшін пайдаланады. Схемадағы барлық тармақтар санын n_в,ондатүрған ток көздерін N_ит,түйіндерін n_у, контурлардын n_к белгілейік (сур.3.1).

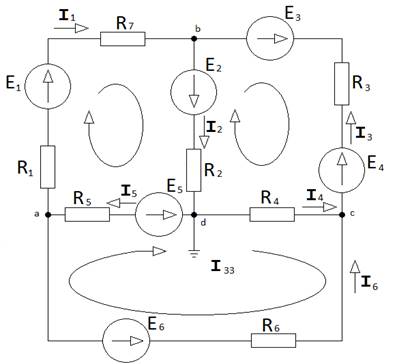
Сур.3.1. Есептеу схемасы

Кирхгофтың бірінші заңы бойынша жазылатын теңдеулердің саны N₁ тәуелсіз түйіндер санына тең. Берілген схема бойынша, әдетте, бір түйін базис түйіні ретінде таңдалады (сур. 3.1 схемасында базис ретінде түйін d жерге қосылған, φ_d =0). Сондықтан тәуелсіз түйіндердің саны жалпы түйіннің санынан бірге кем, яғни N₁= n_у – 1. Сур. 3.1 схема бойынша N₁= 4–1=3 тәуелсіз теңдеулер жазылады.

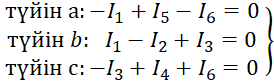(3.1)

Кирхгофтың екінші заңымен жазылатын теңдеулердің саны N₂ тәуелсіз контурлардың саны бойынша анықталады: N₂= n_в –n_у + 1. Сур. 3.1 схема бойынша N₂= 6–4+1=3 тәуелсіз теңдеулер жазылады (контурларды айналу бағытысағат тілімен сәйкес).

1-ші контур: R_1*I₁+ R_7*I₁+ R_2*I₂+R_5*I₅= E₁+ E₂– E₅

2-ші контур: - R_2*I₂– R_3*I₃– R_4*I₄= - E₂+ E₃– E₄ (3.2)

3-ші контур: - R_5*I₅+ R_4*I₄– R_6*I₆= E₅– E₆

(3.1, 3.2) жүйелердін теңдеулерің бірге шешкенде барлығы тармақтар үшін токтардын күші табылады.

3.2. Контурлық токтар әдісі

Электротехникада Кирхгоф заңдарынан шығарған басқа есептеу әдістері бар. Контурлық токтар әдісінде схеманың әрбір тәуелсіз контурында өзінің контурлық тогы жүруге тиыс деп есептейді. Сур. 3.1 схемада І₁₁, І₂₂, І₃₃контурлық токтар болса, тармактардың токтары контурлық токтар алгебралық қосындысымен анықталады:

I₁= І₁₁

I₂= І₁₁- І₂₂

I₃= - І₂₂(3.3)

I₄= - І₂₂+ І₃₃

I₅= І₁₁– І₃₃

I₆= І₃₃

Олай болса Кирхгофтын екінші заңымен құрылған теңдеулер жүйесі (3.2) былай жазылады:

(R₁+ R₇)_*I₁₁+ R_2*(І₁₁- I₂₂)+R_5*(І₁₁– I₃₃)= E₁+ E₂– E₅

- R_2*(І₁₁- I₂₂)– R_3*(-I₂₂)– R_4*(- І₂₂+ І₃₃)= - E₂+ E₃– E₄

- R_5* (І₁₁– I₃₃)+ R_4* (- І₂₂+ І₃₃) – R_6*I₃₃= E₅– E₆

Немесе

R_11*I₁₁+ R₁₂ _* I₂₂+R_13*I₃₃= E₁₁

R_21*І₁₁+ R₂₂ _* I₂₂+R_23*I₃₃= E₂₂(3.4)

R_31*I₁₁+ R₃₂ _* I₂₂+R_33*I₃₃= E₃₃

Контурлық ток теңдеулердің жүйесінде (3.4)

R₁₁= R₁+R₇+R₂+R₅, R₂₂= R₂+R₃+R₄, R₃₃= R₅+R₄+R₆ – тәуелсіз контурдың өздік кедергілері;

R₁₂= R₂₁= - R₂, R₁₃= R₃₁= - R₅, R₂₃= R₃₂= - R₄ – контур аралық кедергілер, яғни екі тәуелсіз контурларға ортақ тармақтардың кедергілері;

Е₁₁= E₁+ E₂– E₅, Е₂₂= - E₂+ E₃– E₄, Е₃₃= E₅– E₆ – контурлық ЭҚК, контурды құрайтын тармақтардың ЭҚК-ің алгебралық қосындысымен анықталады.

(3.4) жүйені есептеп, контурлық токтарды тапқан кейін, (3.3) жүйенең тармақтардағы токтарды табуға болады.

3.3. Түйіндік потенциалдар әдісі

Егер тізбек түйіндардың потенциалдары белгілі болса (сур. 3.1 φ_a, φ_b, φ_c, φ_d), тармақтардын токтары Ом заңынан табылады:

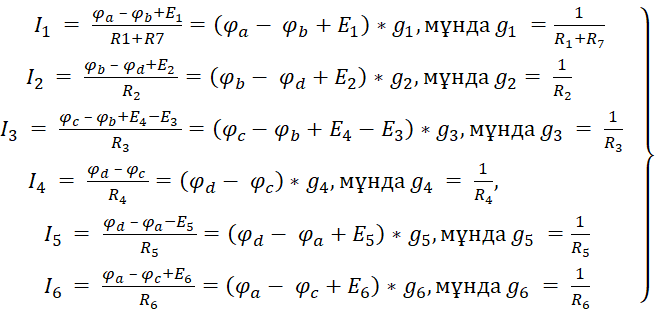(3.5)

Олай болса Кирхгофтын бірінші заңымен құрылған теңдеулер жүйесі (3.1) былай жазылады:

-(φ_a– φ_b + E₁)_*g₁+ (φ_d– φ_a – E₅)_*g₅-(φ_a– φ_c + E₆)_*g₆= 0

(φ_a– φ_b + E₁)_*g₁- (φ_b– φ_a + E₂)_*g₂+(φ_c– φ_b + E₄– E₃)_*g₃= 0

-(φ_c– φ_b + E₄– E₃)_*g₃+ (φ_d– φ_c)_*g₄+(φ_a– φ_c + E₆)_*g₆= 0

Бір түйіның потенциалды нөлге тең ғылып (φ_d = 0), түйіндік потенциалдар әдісінің теңдеулер жүйесін қабылдаймыз:

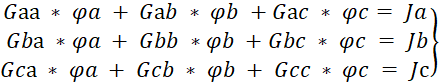(3.6)

Түйіндық потенциалдар теңдеулердің жүйесінде (3.6)

G_аа = g₁+g₅+g₆, G_bb = g₁+g₂+g₃, G_cc = g₃+g₄+g₆ – түйіндердің өздік өткізгіштігі деп аталады да, түйінмен байланысқан тармақтардың өткізгіштерінін қосындысымен анықталады және әрқашанда оң таңбасымен жазылады;

G_аb = G_bа = - g₁, G_аc= G_cа= - g₆, G_bc= G_cb = - g₃– түйін аралық өткізгіштер деп аталады, яғни екі түйінді қосатын тармақттың өткізгіштігі, олар әрқашанда теріс таңбасымен жазылады;

J_a = - E_1*g₁– E_{5 *}g₅– E_{6 *}g₆, J_b = E_1*g₁– E_{2 *}g₂+(E₄– E₃)_*g₃, J_c =(E₂– E₄)_*g₃+ E_6
*g₆– түйіндік токтары деп аталады. Бұл токтын қосындысы E_*g «+» таңбамен алынады, егер ЭҚК түйінге кіретін болса; шығатын болса E_*g «-» таңбамен алынады.

(3.6) жүйені есептеп, түйіндік потенциалдарды тапқан кейін, (3.5) жүйенең тармақтардағы токтарды табуға болады.

3.4. Екі түйінд әдісі

Бұл әдісті екі түйінге жинақталатын бірнеше параллель тармақтары бар

тізбекке, сондай-ақ қарапайым түрлендірулер нәтижесінде екі түйіні бар

тізбекке келтіруге болатын электрлік тізбектерге қолданған жөн (сур.3.2).

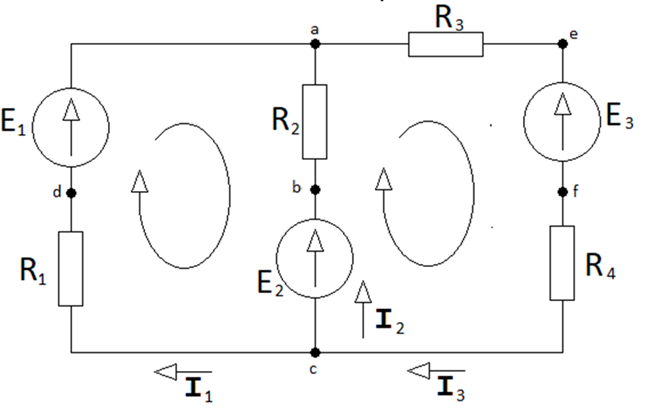
Cур. 3.2. Екі түйінді электр тізбек

Белгілі ЭҚК және кедергілер мәндерімен тармақтық токтарды өрнектен тізбектің түйіндері арасындағы кернеуді есептеу арқылы оңай анықтауға болады. Кирхгоф заңдарын қолданып, түйінаралық кернеу мына түрде алынады:

, (3.7)

мұнда U – түйінаралық кернеу;

– тармақтың жалпы ЭҚК және өткізгіштігінің көбейтінділерінің алгебралық қосындысы;

– тармақ өткізгіштігілерінің қосындысы.

Таңба тандау ереже: Алгебралық қосындыда берілген тармақтың жалпы ЭҚК және өткізгіштігінің көбейтіндісі, егер ЭҚК потенциалы жоғары түйінге бағытталса «+» белгісімен, ал ЭҚК потенциалы төмен түйінге бағытталған болса «-» белгісімен алынады.

Мысал: Тізбек үшін тармақтардың өткізгіштіктері (3.2-сурет) тармақтың жалпы кедергісінің өзара мәндері ретінде анықталады:

, , .

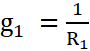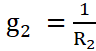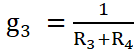3.7 формуласы бойынша түйінаралық кернеу:

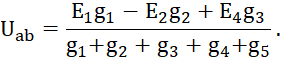
Жалпыланған Ом заңы бойынша тармақтық токтар:

I₁= (E₁- U_ab) g₁, I₂ = (- E₂- U_ab) g₂,I₃ = - U_ab g₃.

Екі түйінді әдіс - түйіндік потенциал әдісінің ерекше жағдайы.

3.5. Эквивалентті генератор әдісі

Эквивалентті генератор әдісі тек бір тармақтың ток күшін оның кедергісі мен ЭҚК әртүрлі мәндерінде білу қажет болғанда қолданылады. Бір тармақ қандай да бір күрделі электр тізбегінен оқшауланғанда, соңғысы тізбектің қалған бөлігіне екі қысқышпен қосылады. Полюстер деп аталатын екі арнайы қысқыштары бар электр тізбегінің бөлігі екіполюстік деп аталады (3.3 -сурет).

Электр энергиясының көздері бар екіполюстік активті, ал көздері жоқтар пассивті деп аталады. Кез келген пассивті екіполюстік электр энергиясын тұтынушы болып табылады, сондықтан эквивалентті тізбекте ол бір элементпен ұсынылуы мүмкін - екіполюстігің кіріс кедергісі деп аталатын R_вх.

Эквивалентті генератор әдісі активті екіполюстік теоремаға негізделген. Оған сәйкес, активті екіполюстік зерттелетін тармаққа әсерін (3.3 а-сурет) эквивалентті генератор арқылы шығаруға болады (3.3 б-сурет). Оның ЭҚК Е_экв ажыратылған тармақтың қысқыштарындағы бос жұріс кернеуіне U_ab _xx тең (3.3 в-сурет), ал ішкі кедергісі R_экв тең a және b полюстерінің жағынан екіполюстігің кіріс кедергісіне R_вх.

Жалпы жағдайда, зерттелетін тармақта R кедергісі және тізбекті жалғанған ЭҚК Е көзі болса, тармақтағы кедергі ЭҚК алдындағы «+» немесе «-» белгілері болатын өрнектен анықталады. көзі бар тармақ үшін Ом заңына сәйкес таңдалады:

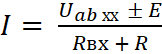(3.8)

және R_вх параметрлерін тәжірибе жүзінде де, есептеу арқылы да анықтауға болады. Бірінші жағдайда екіполюстігің бос жүріс тәжірибесінен (3.3 в-сурет) ажыратылған қысқыштардағы кернеуді анықтау үшін вольтметр қолданылады, ал қысқа тұйықталу тәжірибесінен І_кз ток күшін анықтау үшін амперметр a және b арасына қосылады (3.3 г-сурет). Кіріс кедергісі мынаған тең:

R_вх 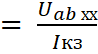. (3.9)

Есептеу тәртібі

1. Берілген электр тізбегінің схемасында зерттелетін тармақты таңдап, ондағы ток пен кернеудің оң бағыттарын таңдаңыз.

2. Таңдалған тармақты тізбектен алып тастап, тізбектің қалған бөлігі үшін екіполюстігің қысқыштарындағы U_{ab xx}кернеуін анықтаңыз.

3. Таңдалған тармақтың терминалдарына қатысты екі терминалды желінің R_вх кедергісін есептеңіз.

4. 3.8 формуласы бойынша қажетті I токты анықтаңыз.

Мысал. 3.2-суретте көрсетілген схема үшін ток I₂ мәнін табыңыз.

Шешім. 1. Түпнұсқа схемада (3.2-сурет) тармақтарының өткізгіштіктері белгілі немесе есептелуі мүмкін, қажетті тармақты өшіреміз.

2. Алынған тізбек үшін (3.3-сурет) эквивалентті генератордың параметрлерін анықтаймыз:

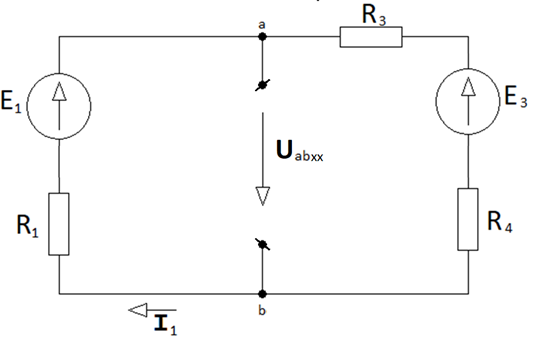
Cур. 3.3. Эквивалентті генератордың параметрлерін анықтау схемасы

3. Эквивалентті генератордың қысқыштарына қашықтағы тармақты қосу арқылы (3.4-сурет) Ом заңы бойынша қажетті токты табамыз:

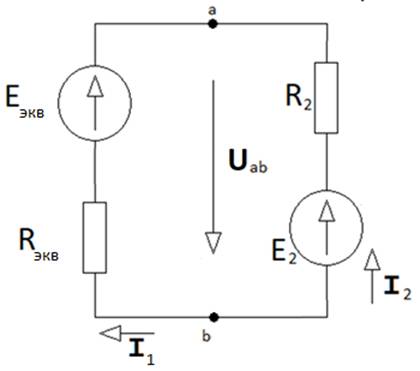
Cур. 3.4. Эквивалентті генераторы бар тізбек