Дәріс 2. Электр тізбектердің заңдары мен түрлендіру
2.1 Электр тізбектердің заңдары
2.1.1. Ом заңы
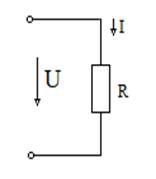 1.6 суретті жаңадан өндіру
етсек шартты-графикалық белгілермен (жалғыз энергия көзі көп кезде
көрсетілмейді, сур.2.1), бұл схемаға Ом заңды пайдалауға болады:
1.6 суретті жаңадан өндіру
етсек шартты-графикалық белгілермен (жалғыз энергия көзі көп кезде
көрсетілмейді, сур.2.1), бұл схемаға Ом заңды пайдалауға болады:
I = ![]() .
(2.1)
.
(2.1)
Тізбектің бөліміңде токтын күші тұра пропорционалды кернеуге және кері пропорционалды бөлімінің кедергісіне.
Сур. 2.1.
Егер бөлімінің ішінде бір-неше тізбекті қосылған ЭҚК мен кедергілер болса (сур.2.2), онда жалпыланған (толық) Ом заңды пайдалауға болады:
Тармақталмаған тізбектін бөлігінде токтын күші тең бөлігінің басы мен аяқ арасындағы кернеуге қосып алған ЭҚК алгебралық қосындысын кедергілерін қосындысына бөлу:
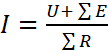 ,
(2.2)
,
(2.2)
мұнда U – бөлігінін кернеу;
![]() –
ЭҚК-ін алгебралық қосындысы;
–
ЭҚК-ін алгебралық қосындысы;
![]() –
бөлігіндегі кедергілерін қосындысы.
–
бөлігіндегі кедергілерін қосындысы.
Таңба тандау ереже: Алгебралық қосындысында ЭҚК «плюс» таңбамен алынады, егер ЭҚК мен токтын бағыттары бірдей болса. Бұл бағыттары қарама қарсы болса, ЭҚК «минус» таңбамен алынады.
Үлгі:
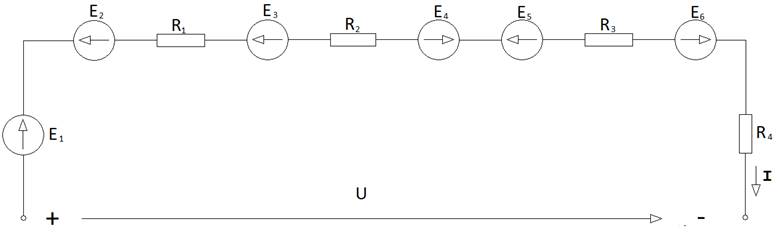
Сур.2.2. Тармақталмаған электр тізбек
Жалпыланған (толық) Ом заңы сур.1.8 схемасына былай жазылады:
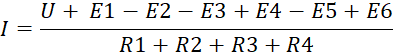
2.1.2. Кирхгофтын бірінші заңы
Ом заңы тізбектің бір бөлігі үшін ғана пайдаланады. Ал бір-бірмен қосылған бірнеше бөлікпен тұратын күрделі электр тізбегі үшін Кирхгоф заңдары пайдаланады. Ол үшін логикалық түсініктемелермен танысу керек:
1) Тармақ – элементтері (E, R) кезекпен-кезек қосылған қиылымсыз электр тізбектің бөлігі, бір ғана ток өтетін (сур. 2.1, 2.2);
2) Түйін – үш немесе одан да көп тармақтарды қосатын электр тізбектің нүктесі (сүр. 2.3);
3) Контур – электр тізбектің тармақтар және түйындармен өтетін түйықталу жол.
Кирхгофтын 1 заңын классиклық тұжырымдасы –
 Бір түйінмен байланысқан тармақтардың
токтардын алгебралық қосындысы нөльге тең болады:
Бір түйінмен байланысқан тармақтардың
токтардын алгебралық қосындысы нөльге тең болады:
![]() .
(2.3)
.
(2.3)
Таңба тандау ереже: Алгебралық қосындысында түйынға құйылатын токтар бір таңбамен (мысалы «плюс» пен) алынады, түйынан шығатын токтар кері таңбамен (мысалы «минус» пен) алынады.
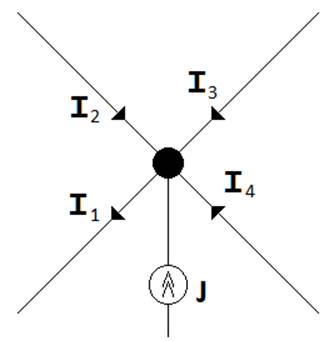
Сур. 2.3 көрсетілген түйынға тендеу
Сур. 2.3. Түйын (2.3) былай жазылады:
I1 – I2 – I3 +I4 +J = 0. (2.4)
Минусы бар токтарды (2.4) тендеудің оң жаққа көшіргенде
I1 +I4 +J = I2 + I3. (2.5)
Бұдан (2.5) Кирхгофтын 1 заңын жалпыланған тұжырымдасы туады:
Түйынға кіретін токтардын қосындысы тең түйынан шығатын токтардын қосындысына.
2.1.3. Кирхгофтын екінші заңы
Кедергіні R сол кедергімен өтетің токтын күшіне I көбейткенде болып шыққан көлемді кернеудің түсуі R*I деп атайды. Кирхгофтын екінші заңын да екі түрлі жолмен тұжырымдауға болады.
1) Түйық контурдың бойындағы кернеулердің алгебралық қосындысы нөлге тең:
![]() (2.6)
(2.6)
2.4 суреттегі схеманың оң жақты контурды сағат тілімен сәйкес
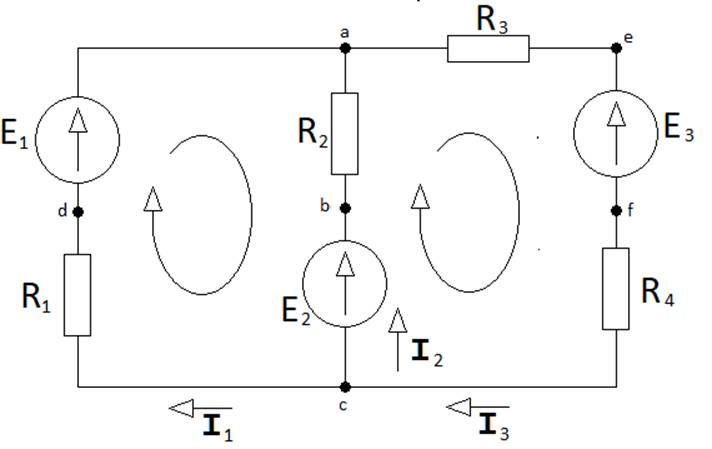
Cур. 2.4. Тармақталған электр тізбек
айналғанда, (2.6) былай ашылады:
Uae +Uef +Ufc +Ucb +Uba = 0.
2) Түйық контурдың кернеудің түсунің алгебралық қосындысы осы контур бойындағы барлық ЭҚК-нің алгебралық қосындысына тең болады:
![]() (2.7)
(2.7)
2.4 суреттегі схеманың контурлар үшін
R1*I1 – R2*I2 = E1 – E2
R2*I2 – R3*I3 – R4*I3 = E2 – E3.
2.2. Тұрақты ток тізбегіндегі электр қуаты
Электр тізбегінің қимасы арқылы өтетін ток ағыны деп осы бөлімдегі кернеу u әсерінен зарядтың q қозғалысын айтады. Сонымен бірге dt уақыттың әрбір элементар кезеңінде элементар жұмыс dw орындалады:
dw = u ![]() dq.
dq.
Энергияның уақыт бойынша туындысы, былайша айтқанда, берілген уақыт мезгілінде тізбекке электр энергиясының түсу жылдамдығы лездік қуаттың шамасың береді. Демек, лездік қуаттың шамасы p [Вт] лездік ток және кернеудің көбейтіндісіне тең:
p
= ![]() =
u
=
u ![]() i.
(2.8)
i.
(2.8)
Тұрақты ток тізбегіндегі кернеу мен ток күші уақытымен өзгермейтіндіктен, тізбектің қуаты оның лездік мәніне тең болып қалады және (2.8) өрнек мынадай түрімен жазылады:
P
=U ![]() I
(2.9)
I
(2.9)
Егер энергия көзі ЭҚК көзі болса (сур. 1.6а), онда қысқыштардағы кернеу ЭҚК-ен бірдей (E = U) және ол шығаратын қуаты тең, (2.9) сәйкес, ЭҚК және сол көзінен өтетін токтың күшіне көбейтіндісіне:
Pг
=Е ![]() I
(2.10)
I
(2.10)
Егер энергия көзі ток көзі болса (сур. 1.6б), онда І = J, және ол шығаратын қуаты тең, (2.9) сәйкес, көзінің қысқыштардағы кернеу және көзінің ток күшіне көбейтіндісіне:
Pг
=U ![]() J
(2.11)
J
(2.11)
(2.10, 2.11) формулаларда токтың оң бағыты кернеу мен ЭҚК оң бағытымен сәйкес келсе, қуат оң болады, 1.6 суретте көрсетілген. Бұл жағдайда көз тізбекке электр энергиясын жасайды (береді). Әйтпесе, қуат теріс болады және көз тізбектен энергияны тұтынады (қабылдайды).
Ток резистор арқылы өткенде кернеу Ом заңы бойынша R*I түрінде анықталады. Сонда (2.9) сәйкес резисторға бөлінген қуат мынаған тең:
Pж
=I2![]() R
(2.12)
R
(2.12)
Электр тізбегіне қатысты энергияның сақталу заңы көздермен өндірілетін жалпы қуат пен электр жүктемесі тұтынатын жалпы қуаттың теңдігімен табылады. Өндірілген және тұтынылатын қуаттың теңдігі Pг = Pж тізбектің қуат балансы деп аталады.
Көздердің жалпы қуаты ЭҚК өнімдерінің алгебралық қосындысы және ол арқылы өтетін ток күші, сонымен қатар ток көздерінің кернеуі және көздің ток күші өнімдерінің алгебралық қосындысы ретінде анықталады:
Pг
=![]() (2.13)
(2.13)
Алгебралық қосындыда ![]() ЭҚК көзінің
қуаты E
ЭҚК көзінің
қуаты E![]() I,
егер ЭҚК мен токтың оң бағыттары сәйкес келсе, плюс белгісімен, ал басқа
жағдайда минус белгісімен қабылданады. Сол сияқты, алгебралық қосындыда
I,
егер ЭҚК мен токтың оң бағыттары сәйкес келсе, плюс белгісімен, ал басқа
жағдайда минус белгісімен қабылданады. Сол сияқты, алгебралық қосындыда ![]() ток көзінің
қуаты U
ток көзінің
қуаты U![]() I,
егер көздің кернеуі мен токының оң бағыттары сәйкес келсе плюс белгісімен, ал
басқа жағдайда минус таңбасымен қабылданады.
I,
егер көздің кернеуі мен токының оң бағыттары сәйкес келсе плюс белгісімен, ал
басқа жағдайда минус таңбасымен қабылданады.
Жалпы жүктеме қуаты тізбектің барлық кедергілеріне бөлінген қуаттардың қосындысына тең:
Pж
= ![]() I2
I2
![]() R
(2.14)
R
(2.14)
Осылайша, шарт бойынша тізбектегі қуат балансы байқалады
![]() =
= ![]() I2
I2![]() R.
(2.15)
R.
(2.15)
Мысал ретінде тізбек үшін қуат балансын жазайық (2.4-сурет):
Е1*I1+ Е2*I2- Е3*I3 = I12* R1 + I22* R2 + I32* R3 + I32* R4.
2.3 Тізбекті эквивалентті түрлендіру
Екі схеманы эквивалентті деп аталады, егер сыртқы полюстарының токтары мен кернеулері өзгермей қалатын болса. Тізбектітеліп қосылған схеманың эквиваленттік кедергісі Rэ барлық кедергілердің арифметикалық қосындысымен анықталады (сур.2.5 а).
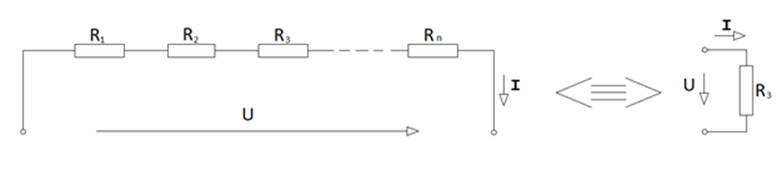
Rэ = R1+R2+R3…+Rn. (2.16)
a)
ал эквиваленттік ЭҚК – алгебралық қосындысымен анықталады (сур.2.5 б).
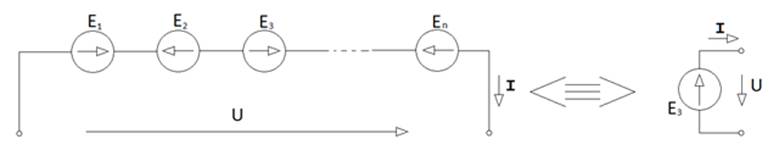
Еэ = Е1 - Е2+Е3 …- Еn. (2.17)
б)
Сур.2.5. Тізбектеп қосу
Тізбектің элементтері параллель қосылған кезінде эквиваленттік өткізгіштігі gэ арифметикалық қосынды түрінде анықталады (сур.2.6 а),
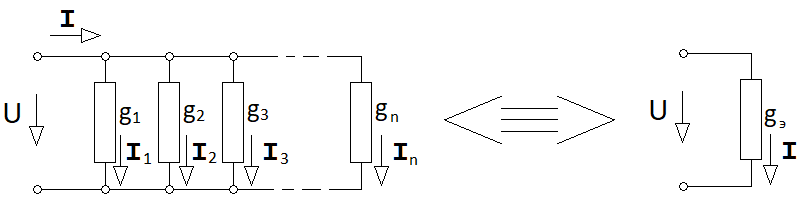
gэ = g1+g2+g3 …+gn. (2.18)
a)
ал токтары алгебралық қосынды түрінде анықталады (сур.2.6 б).
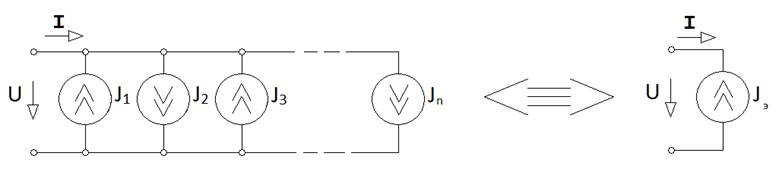
Jэ = J1 - J2+J3 …- Jn . (2.19)
б)
Сур.2.6. Параллель қосу
ЭҚК көзі эквивалентті ток көзіне және
керсінше түрленеді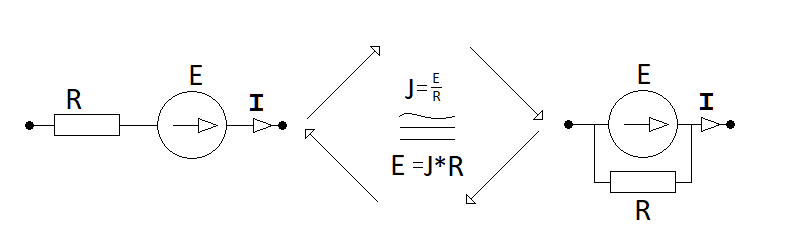
Жұлдыз схемасының (сур.2.7) үшбұрышқа түрленуі:
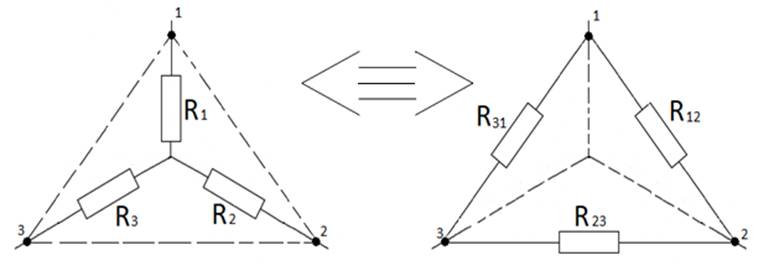
Сур.2.7. Жұлдыз бен үшбұрыш схемалары
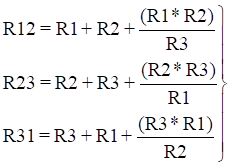
![]() (2.20)
(2.20)
Үшбұрыш схемасының жұлдызға түрлендіруі:
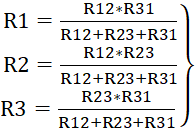 (2.21)
(2.21)