Практическое занятие 11.2.

Комбинационная группировка

В некоторых задачах результативных признаков может быть несколько, как правило, два, например: X - выпуск продукции, - прибыль и - себестоимость производства. Никаких проблем - сортируем совокупность по признаку-фактору X (выпуску продукции), при этом в таблице нужно выделить не два, а уже три столбца. Далее выполняем группировку и рассчитываем средние значения прибыли и себестоимости по каждой группе. Делаем выводы. Заметим, кстати, что корреляционная связь , вероятно, обратная, поскольку при увеличении выпуска продукции, издержки могут падать (ввиду автоматизации процесса при массовом производстве).

Комбинационная группировка - это группировка статистической совокупности совместно по двум или большему количеству признаков. Она позволяет выявить устройство совокупности и установить взаимосвязи между её признаками.

Рассмотрим выборку, состоящую из п = 100 котов, среди которых оказалось 20 грациозных (менее 4 кг), 50 обычных (4-6 кг) и 30 толстых (более 6 кг). По существу, перед нами структурная группировка животных по их массе, и это первый признак статической совокупности. Теперь возьмём какой-нибудь второй признак, например, разделим всех котов на злых и добрых:) Признак, кстати, качественный, но при желании его можно «оцифровать», рассмотрев некую экспертную шкалу доброты.

В результате исследования выяснилось, что среди тощих котов 14 злых и 6 добрых, среди обычных - 24 злых и 26 добрых и среди толстых - 7 злых и 23 добрых.

Очевидно, что между этими признаками есть связь. Чем больше масса кота, тем более вероятно, что он окажется добрым. Ибо с лишним весом, полным желудком и злиться весьма проблематично. Однако и среди толстых котов тоже есть особи с проблемным характером. Такая нежёсткая зависимость называется корреляционной.

Полученные данные обычно сводят в комбинационную таблицу:

Масса кота, кг, X	Характер кота, Y		Итого,
	Злой	Добрый
менее 4	14	6	20
4 – 6	24	26	50
более 6	7	23	30
Итого,	45	55	100

Внимательно изучаем таблицу и обозначения:

1) Признак-фактор X (причину) и его категории располагают в левом столбце (зелёный цвет), а признак-результат Y (следствие) и его категории - в «шапке» таблицы (жёлтый цвет). Встречается и расположение.

2) В основной части таблицы (серый цвет) располагаются собственно результаты группировки - совместные групповые частоты . Итак, у нас в наличии есть:

 тощих и злых и  тощих и добрых котов;

 обычных и злых и  обычных и добрых котов;

 толстых и злых и  толстых и добрых котов;

Итого: 6 групп.

Справка: первый подстрочный индекс означает номер строки (рассматриваем серую область), а второй - номер столбца. Так, значение, расположено в 1-й строке, 2-м столбце, а значение - в 3-й строке, 1-м столбце.

Сумма всех групповых частот равна объёму статистической совокупности:

.

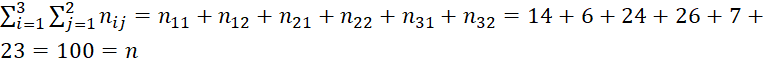Заканчиваем разбор таблицы:

3) В правом столбце (зелёный цвет) располагаются суммы по строкам (по группам признака-фактора). В нашей совокупности имеется  грациозных,  обычных и  толстых котов. Итого:  особей.

В нижней строке (жёлтый цвет) подсчитываем суммы по столбцам (по категориям признака-результата):  злых и добрых котов. Итого: , в чём и требовалось убедиться.

Общая сумма (объём совокупности) находится в правом нижнем углу: п = 100 .

Может ли в комбинационной группировке быть большее количество факторов? Да. Так, в нашем примере можно добавить фактор Z - жилищные условия кота (бездомный или домашний). В результате получится трёхмерная комбинационная группировка с группами:

тощие, злые и бездомные коты;

тощие, злые и домашние коты;

тощие, добрые и бездомные коты;

тощие, добрые и домашние коты;

обычные, злые и бездомные коты;

…

и так далее, всего 12 групп.

Теперь переходим к решению стандартной задачи, в которой предлагается простейшая двумерная комбинационная группировка.

Задача 1.

Имеются выборочные данные о выпуске продукции (млн. руб.) и сумме прибыли (млн. руб.) по 30 предприятиям:

Номер предприятия	Выпуск продукции	Прибыль	Номер предприятия	Выпуск продукции	Прибыль
1.	65	15,7	16.	52	14,6
2.	78	18	17.	62	14,8
3.	41	12,1	18.	69	16,1
4.	54	13,8	19.	85	16,7
5.	66	15,5	20.	70	15,8
6.	80	17,9	21.	71	16,4
7.	45	12,8	22.	64	15
8.	57	14,2	23.	72	16,5
9.	67	15,9	24.	88	18,5
10.	81	17,6	25.	73	16,4
11.	92	18,2	26.	74	16
12.	48	13	27.	96	19,1
13.	59	15,5	28.	75	16,3
14.	68	16,2	29.	101	19,6
15.	83	16,7	30.	76	17,2

Определить признак-фактор и признак-результат и высказать предположение о наличии и направлении корреляционной зависимости между признаками. Выполнить комбинационную группировку, разбив значения признака-фактора на 5 равных интервалов, а значения признака-результата - на 3 интервала. Сделать выводы.

Числовые данные мы взял из задачи прошлого практического занятия. Мы выяснили, что признаком- фактором (причиной) является X - выпуск продукции, а признаком-результатом (следствием) Y - прибыль предприятий. При увеличении выпуска продукции, очевидно, растёт средняя прибыль предприятий, таким образом, предполагаемая корреляционная зависимость - прямая («чем больше, тем больше»).

Начало решения совпадает с началом разобранной задачи. Упорядочим предприятия по возрастанию признака-фактора. Далее мы нашли размах вариации

 млн. руб.

и разбили значения признака-фактора на 5 равных интервалов. Длина каждого интервала составила млн. руб., после чего у нас получились следующие группы:

Группа 1, выпуск 41-53 млн. руб.		Группа 2, выпуск 53-65 млн. руб.		Группа 3, выпуск 65-77 млн. руб.		Группа 4, выпуск 77-89 млн. руб.		Группа 5, выпуск 89-101 млн. руб.
Выпуск	Прибыль	Выпуск	Прибыль	Выпуск	Прибыль	Выпуск	Прибыль	Выпуск	Прибыль
41	12,1	54	13,8	65	15,7	78	18	92	18,2
45	12,8	57	14,2	66	15,5	80	17,9	96	19,1
48	13	59	15,5	67	15,9	81	17,6	101	19,6
52	14,6	62	14,8	68	16,2	83	16,7
		64	15	69	16,1	85	16,7
				70	15,8	88	18,5
				71	16,4
				72	16,5
				73	16,4
				74	16
				75	16,3
				76	17,2
Количество предприятий в группах,
4		5		12		6		3

Теперь в каждой группе нужно выделить подгруппы, условно говоря, предприятия с небольшой, средней и высокой прибылью (3 интервала по условию). Для этого берём исходные значения признака-результата (прибыли) и сортируем их по возрастанию. Для компактности расположу упорядоченные значения в три колонки:

Прибыль
12,1	15,7	16,7
12,8	15,8	16,7
13	15,9	17,2
13,8	16	17,6
14,2	16,1	17,9
14,6	16,2	18
14,8	16,3	18,2
15	16,4	18,5
15,5	16,4	19,1
15,5	16,5	19,6

С простейшей сортировкой, проблем уже ни у кого нет. Но напоминаем последовательность решения:

Вычислим размах вариации:  млн. руб. и длину каждого интервала: , как удачно разделилось! В результате получилось три интервала прибыли: 12,1 – 14,6; 14,6 – 17,1 и 17,1 – 19,6 млн.руб.

Теперь в групповой таблице красными галочками помечаем предприятия 1-го интервала, зелёными - предприятия 2-го интервала и синими - 3-го интервала:

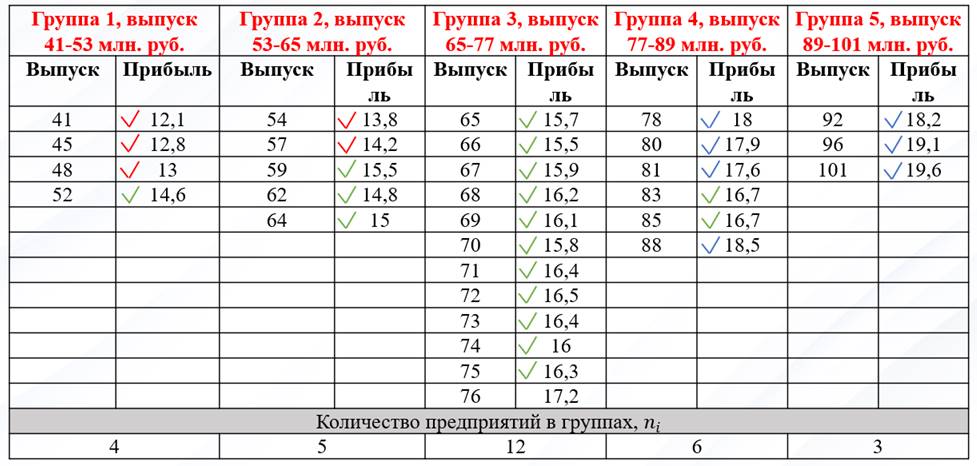
По каждой из 5 групп подсчитываем количество предприятий с небольшой (красной), средней (зелёной) и высокой (синей) прибылью. Результаты сведём в комбинационную таблицу, при этом значения признака-фактора удобно расположить по горизонтали - в «шапке» таблицы, а значения признака-результата слева по вертикали:

Прибыль Y, млн. руб.	Выпуск продукции X, млн. руб.
	41-53	53-65	65-77	77-89	89-101
12,1-14,6	3	2
14,6-17,1	1	3	11	2
17,1-19,6			1	4	3

Следует заметить, что построение комбинационной группировки можно автоматизировать (например, в МS Ехсе1), но в простейших учебных примерах проще выполнить ручной подсчёт частот.

Частота n₁₂=2 означает, что у нас есть два предприятия с выпуском продукции 53-65 млн. руб. и невысокой прибылью (12,1-14,6 млн. руб.). Частота n₃₄=4 означает, что в выборке 4 предприятия с выпуском продукции 77-89 млн. руб. и высокой прибылью (17,1-19,6 млн. руб.).

Для самоконтроля подсчитываем суммы по серым столбцам: n₁=3+1=4,   n₂=2+3=5,   n₃=11+1=12,    n₄=2+4=6,   n₅=3,

всего:  предприятий. Результаты заносим в нижнюю строку (см. таблицу ниже).

И самое интересное - суммы по серым строкам:

предприятий с небольшой прибылью;

предприятий со средней прибылью;

предприятий с высокой прибылью.

Итого: , что и требовалось проверить. Результаты заносим в правый столбец.

Таким образом, итоговая комбинационная таблица выглядит следующим образом:

Прибыль Y, млн. руб.	Выпуск продукции X, млн. руб.					Итого,
	41-53	53-65	65-77	77-89	89-101
12,1-14,6	3	2				5
14,6-17,1	1	3	11	2		17
17,1-19,6			1	4	3	8
Итого,	4	5	12	6	3	30

Сделаем выводы. Смотрим, как располагаются частоты (числа в серой области).

Если частоты имеют тенденцию располагаться по диагонали от левого верхнего до правого нижнего угла, то между признаками существует прямая корреляционная зависимость («чем больше, тем больше»). Это наш случай - по таблице хорошо видно, что с увеличением выпуска продукции растут и средние прибыли предприятий. Готово.

Если частоты имеют тенденцию располагаться по диагонали от левого нижнего до правого верхнего угла, то между признаками существует обратная корреляционная зависимость («чем больше, тем меньше»).

И, наконец, если частоты расположены хаотично, без явной закономерности, то корреляционная зависимость отсутствует либо является слабой.

Контрольные вопросы

1. Комбинационная таблица

2. Совместные групповые частоты

3. Признак-фактор, признак-результат

4. Комбинационная группировка