Тәжірибелік тапсырманы орындау үшін тәжрибелік жоспарлау

НЕГІЗГІ ҰҒЫМДАР МЕН АНЫҚТАМАЛАР

Оңтайландыру мәселелерін шешуге арналған эксперименттер экстремалды деп аталады. Төтенше есепті шешу үшін зерттелетін объектінің математикалық моделі болуы қажет. Математикалық модель-оқып жатқан процесті немесе құбылысты сипаттайтын математикалық арақатынастар жүйесі.

Бұл атау кейбір функцияның экстремумын оңтайландыру мен іздеудің терең ұқсастығына байланысты. Егер оның мақсаты кейбір функцияның экстремумын іздеуден тұрса, міндет экстремалды болып табылады. Екі тапсырманың қайсысы экстремалды болып табылатынын анықтау үшін олардың тұжырымдарына жүгіну және экстремалдық талаптары қай жерде қанағаттандырылатынын анықтау қажет.

Зерттеу объектісін сипаттау үшін күрішке схемалық түрде бейнеленген кибернетикалық жүйе туралы түсінікті пайдалану ыңғайлы (Сурет 1).

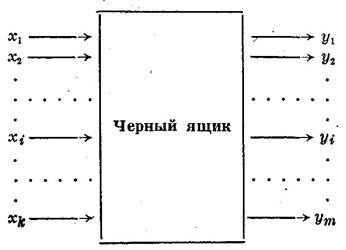
Сурет 1. Қара жәшіктің схемасы

Мұндай кибернетикалық жүйені "қара қорапша"деп атайды. Оң жақ көрсеткілер зерттеу мақсаттарының сандық сипаттамаларын бейнелейді. Біз оларды Y әрпімен белгілейміз және оңтайландыру параметрлері деп атаймыз. Әдебиетте басқа атауларды кездестіруге болады: оңтайландыру критерийі, мақсатты функция, "қара жәшіктің" шығуы және т. б.

Эксперимент жүргізу үшін "қара жәшіктің" мінез-құлқына әсер ету мүмкіндігі болуы керек. Мұндай әсердің барлық жолдарын X әрпімен белгілеп, факторлар деп атаймыз. Олар сондай-ақ "қара жәшіктің"есіктері деп аталады. Есепті шешу кезінде зерттеу объектісінің математикалық модельдерін қолданамыз.

Экспериментті жоспарлау кезінде математикалық модель ретінде оңтайландыру параметрін факторлармен байланыстыратын теңдеуді түсінеді. Мұндай теңдеу де жауап беру функциясы деп аталады.

Экстремалды эксперименттерді қою кезінде бірінші кезеңде Оптимум аймағын табады. Екінші кезеңде Оптимум аймағында жауап беті туралы толық түсінік алуға тырысады. Қысылтаяң міндетті шешу жауап беру функциясын алуды және оның оңтайлы процесс өту шарттары арқылы табуды көздейді.

Жалпы түрде жауап функциясы h болып табылады және параметроңтайландыру, келесі өрнек ұсынылуы мүмкін:

η = f ()

мұнда тәуелсіз айнымалы факторлар.

Егер жауап беру функциясы белгілі болса, процестің оңтайлы шарттарыэксперимент жасамай, талдау арқылы табады. Алайда, процесс механизмін толық білмеу кезінде экстремалды міндеттерді жиі шешуге тура келеді. Бұл жағдайда жауап функциясының таңдамалы бағасын регрессия теңдеуімен көрсетуге болады

+ ...

мұндағы − тиісті айнымалылардың регрессия коэффициенттері.

Эксперимент нәтижелері бойынша іріктеуді ғана анықтауға боладырегрессияның теориялық коэффициенттерінің бағалары болып табылатын ) регрессиясының коэффициенттері.

Экспериментті жоспарлаудың бірінші кезеңінде оптимумға қозғалыс бағытын анықтау және жауап беті бойынша тік көтерілу үшін жауап функциясы бірінші дәрежелі полиномды білдіреді.

Бокс-Уилсон әдісі бірнеше тәжірибе жүргізуді көздейдіжәне процестің параметрлерін жауап беті бойынша крутой көтерумен оңтайландыруға мүмкіндік береді. Әр серияда бір уақыттабелгілі бір ережелер бойынша барлық факторлар өзгереді. Тәжірибе осылай,алдыңғы серияның нәтижелерін математикалық өңдеуден кейін келесі тәжірибелер сериясын жоспарлауға болады.

Экстремалды экспериментті жоспарлау кезінде зерттеу мақсатынақты тұжырымдалуы және сандық бағасы болуы тиіс.

Төтенше экспериментті жоспарлау кезінде оңтайландыру керек параметрді анықтау өте маңызды. Мұны істеу оңай емес, меніңше, бірінші көзқарас. Зерттеудің мақсаты өте нақты тұжырымдалуы және сандық бағалауға жол беруі тиіс.

Экстремалды эксперименттерді жоспарлаудың математикалық әдістері барлық тәуелсіз айнымалыларды бір уақытта өзгерткен кезде қандай да бір бастапқы шарттардан дәйекті жылжыту арқылы Оптимум аймағын табуға мүмкіндік береді.

Осылайша, экстремалды эксперименттерді жоспарлау градиент бойынша қозғалыс идеясын миогофакторлы регрессиялық эксперименттерді жоспарлаумен біріктіреді.

Спектрлік талдауда экстремалды эксперименттерді жоспарлау әдістерін мынадай міндеттерді шешу үшін пайдаланған жөн: максималды сезімталдықты немесе дәлдікті алу мақсатында спектрлік талдау шарттарын оңтайландыру; талдау нәтижелеріне жалпы құрамның әсерін сипаттайтын үлгілерді пайдалану; жүйелі қателіктерді анықтау және оларды есепке алу; стандартты үлгілердің ұтымды жүйесін құру. Қазіргі уақытта бар жұмыстардың көпшілігінде бірінші міндет шешілуде.

Экстремалды эксперименттерді жоспарлау әдістерін пайдалануға кірісе отырып, оңтайлылық критерийін таңдау қажет. Бұл таңдау өте маңызды, ол, шын мәнінде, алдағы жұмыстың табысты немесе сәтсіздігін анықтайды. Оңтайлылық критерийі (оңтайландыру параметрі) мынадай жалпы талаптарды қанағаттандыруы тиіс: сандық, яғни өсіру.

Экстремалды эксперимент жоспарлаумен танысуға кірісе отырып, оңтайландыру кезінде детерминирленген тәсіл, әсіресе химияда кеңінен қолданылады. Бұл ретте құбылыстар механизмін ( мысалы, кинетиктер, гидродинамиктер) мұқият зерттеу негізінде процестің физикалық моделін құру болжанады, бұл объектінің математикалық моделін дифференциалдық теңдеулер жүйесі түрінде алуға мүмкіндік береді. Әрине, детерминацияланған және статистикалық ( экспериментті жоспарлауға байланысты) тәсілдер кейде қалай жасалатыны сияқты қарсы емес, бір-бірін ақылға қонымды толықтыруы керек.

Спектрлік талдауда экстремалды эксперименттерді жоспарлаудың математикалық әдістерін қолдану мәселелері қарастырылды.

Мұндай жағдайда реакция жылдамдығының белгісіз айнымалылардың мәндеріне эмпирикалық тәуелділігін орнатуға мүмкіндік беретін экстремалды экспериментті жоспарлау әдістері қолданылады.

Төменде қозғалыстың экстремумға бағытын анықтау және қозғалыстың өзін ұйымдастыру тәсілімен ерекшеленетін экстремалды эксперименттерді жоспарлаудың екі типтік әдісі қарастырылған.

Экспериментті жоспарлау теориясында екі негізгі бағыт бар: экстремалды эксперименттерді жоспарлау және құбылыстар механизмін анықтау бойынша эксперименттерді жоспарлау.

Шығыс сигналын алудың оңтайлы шарттарын іздеу үшін экстремалды экспериментті жоспарлау әдістері қолданылады. Бұл ретте пікірді ( оңтайландыру параметрін) таңдау үшін талдау нәтижелерін метрологиялық бағалау бойынша ұсынымдар пайдаланылады. Хемометрика міндеттерінің шеңберіне химиялық метрология, қайталанушылықты және зертханааралық жаңғыртуды бағалау міндеттері кіреді.

Объектінің тіркелген қасиеттері кезінде экстремалды басқару міндеттерінің басқа сыныбы экстремалды эксперименттерді жоспарлау міндеттері болып табылады. Мұнда объект туралы априорлық ақпараттың толық болмауы ерекше болып табылады. Басқару үшін қажетті барлық ақпарат сұралады және тапсырманы шешу барысында алынады. Бұл ретте, әдетте, объект өзгеріссіз қалады деп болжанады.

Бұл тарауда біз төтенше экспериментті жоспарлау теориясында қолданылатын негізгі анықтамалармен таныстық. Экспериментке кіріспес бұрын, оның мақсатын бір мәнді және қарама-қарсы тұжырымдау және Біз оңтайландыру параметрі деп атаған осы мақсаттың лайықты сандық сипаттамасын таңдау қажет.

Төртіншіден, экспериментті жоспарлау теориясы КСРО-да және шет елдерде экстремалды эксперименттерді жоспарлаудың статистикалық әдісі ретінде дамиды. Осылайша, жүргізілген жұмыс келесі кезеңге өту үшін қажетті алғышарттар жасады, ол II реттегі орталық ротатабельді композициялық жоспарлау болып табылады. Ол жоспардың тиісті бөліктеріндегі нүктелер санының табуландырылған мәндері негізінде құрылады.

Экстремалды эксперименттерді жоспарлаудың статистикалық әдісін пайдалана отырып, оларды біріктіру арқылы жоғары тығыздықты фосфоры бар ұқсас полиэтиленге модификация жүргізілді. Оның негізінде болатқа бекітудің жоғары беріктігі бар, сондай-ақ жеткілікті жоғары физика-механикалық қасиеттері бар материалды алу шарттары табылған процестің математикалық моделі жасалды.

Әдістердің бұл тобына экспериментті жоспарлау және оңтайландыру әдістері, атап айтқанда экстремалды эксперименттерді жоспарлау әдістері, кейінге қалдыратын эксперименттерді I шандандыру әдістері, жүйелі симплексті әдіс, жалпыланған өлшемдер мен жалпыланған функциялар әдістері жанасады.

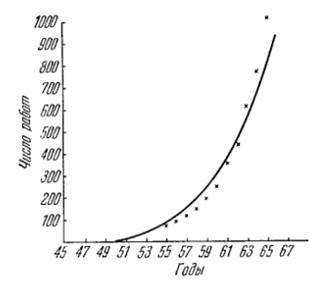
Суретте статистикалық әдістердің бірі - экстремалды эксперименттерді жоспарлау бойынша жұмыстар санының өсу қисығы келтірілген. Мұнда екі есе әр 2-4 жыл сайын болады.

Бұл ретте классикалық регрессионды талдауға негізделген әдістер мен экстремалды эксперименттерді жоспарлау негізделген әдістер ерекшеленеді. Бірінші жағдайда математикалық модель пассивті эксперимент деп аталатын нәтижелерді өңдеу кезінде, әр айнымалылардың кезекпен өзгеруі бар эксперименттердің үлкен сериясы қойылған кезде алынады.